题目内容
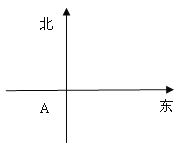
【题目】已知点列
为函数
图像上的点，点列
顺次为
轴上的点，其中
，对任意
，点
构成以
为顶点的等腰三角形.
（1）证明：数列
是等比数列；
（2）若数列中任意连续三项能构成三角形的三边，求
的取值范围；
（3）求证：对任意，
是常数，并求数列
的通项公式.
【答案】（1）证明见解析； （2）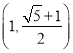
； （3）证明见解析；
【解析】
（1）因为
，所以
，得到
为等比数列；
（2）要使数列
中任意连续三项能构成三角形的三边，根据三角形三边关系得到不等式，解得.
（3）因为
为常数，所以
，
，
，
及
，
，
，
都是公差为2的等差数列，分别求出通项公式即可；
解：（1）
，
，
是以
为首项，
为公比的等比数列
（2）由（1）知
，要使数列中任意连续三项能构成三角形的三边，
即，
，
所以需满足
即
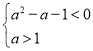解得
即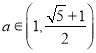
（3）依题意，
，
，
，
，
，
，
，，为常数
，，，
，及，，，都是公差为2的等差数列，
，
，
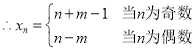
练习册系列答案
阅读快车系列答案
相关题目
