题目内容
设函数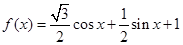
(1)求函数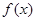 的值域和函数的单调递增区间;
的值域和函数的单调递增区间;
(2)当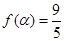 ,且
,且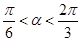 时,求
时,求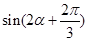 的值.
的值.
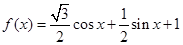
(1)求函数
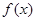 的值域和函数的单调递增区间;
的值域和函数的单调递增区间; (2)当
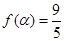 ,且
,且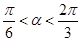 时,求
时,求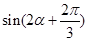 的值.
的值.(1)值域是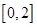 ,增区间为
,增区间为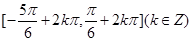 ;(2)
;(2)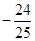 .
.
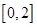 ,增区间为
,增区间为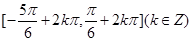 ;(2)
;(2)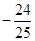 .
.试题分析:本题主要考查两角和的正弦公式、倍角公式、三角函数值域、三角函数单调性等基础知识,考查学生的分析问题解决问题的能力、计算能力.第一问,要求出三角函数的值域,需利用两角和的正弦公式将三角函数式化成单一三角函数,然后利用三角函数的有界性求函数值域,结合
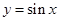 图象,求三角函数的单调递增区间;第二问,先利用
图象,求三角函数的单调递增区间;第二问,先利用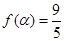 ,求出
,求出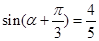 ,通过观察得到
,通过观察得到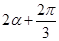 与
与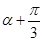 是二倍角关系,所以先通过平方关系,得到
是二倍角关系,所以先通过平方关系,得到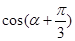 ,再用倍角公式将所求表达式展开,将已知代入求值.
,再用倍角公式将所求表达式展开,将已知代入求值.试题解析:依题意
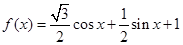
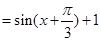 2分
2分(1) 函数
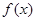 的值域是
的值域是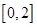 ; 4分
; 4分令
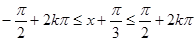 ,解得
,解得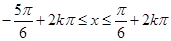 7分
7分所以函数
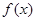 的单调增区间为
的单调增区间为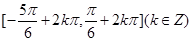 . 8分
. 8分(2)由
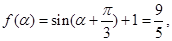 得
得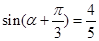 ,
,因为
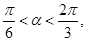 所以
所以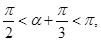 得
得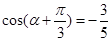 , 10分
, 10分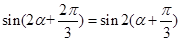
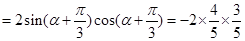
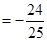 12分
12分
练习册系列答案
相关题目
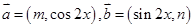 ,函数
,函数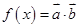 ,且
,且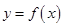 的图像过点
的图像过点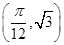 和点
和点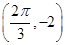 .
. 的值;
的值;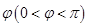 个单位后得到函数
个单位后得到函数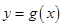 的图像,若
的图像,若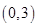 的距离的最小值为1,求
的距离的最小值为1,求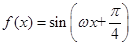 (
(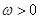 )与函数
)与函数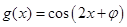 (
(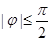 )的对称轴完全相同,则
)的对称轴完全相同,则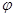 的值为( )
的值为( )



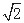 cosx的图象,只需将函数y=
cosx的图象,只需将函数y=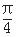 )的图象上所有的点的( ).
)的图象上所有的点的( ).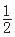 倍(纵坐标不变),再向左平行移动
倍(纵坐标不变),再向左平行移动 个单位长度
个单位长度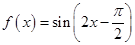 ,则
,则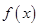 是( )
是( )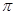 的奇函数
的奇函数 的奇函数
的奇函数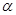 ,使
,使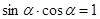 ;
;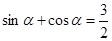 ;
;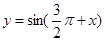 是偶函数;
是偶函数;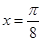 是函数
是函数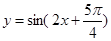 的一条对称轴方程;
的一条对称轴方程;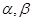 是第一象限角,且
是第一象限角,且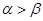 ,则
,则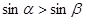 .
.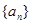 满足
满足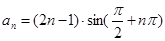 ,则它的前
,则它的前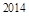 项和等于( )
项和等于( )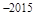
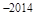
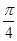 个单位长度,再将所得图象的所有点的横坐标伸长到原来的2倍(纵坐标不变),得到的函数解析式为( ).
个单位长度,再将所得图象的所有点的横坐标伸长到原来的2倍(纵坐标不变),得到的函数解析式为( ).