题目内容
已知f(α)=sin(π-α)cos(2π-α)tan(-α-π)tan(-π+α)sin(-α-π)
(1)化简f(α);
(2)若α是第三象限角,且cos(α-
)=
,求f(α)的值
(3)若α=-1860°,求f(α)的值.
(1)化简f(α);
(2)若α是第三象限角,且cos(α-
| 3π |
| 2 |
| 1 |
| 5 |
(3)若α=-1860°,求f(α)的值.
(1)∵f(α)=sin(π-α)cos(2π-α)tan(-α-π)tan(-π+α)sin(-α-π)
=sinαcosα•(-tanα)[-(-tanα)]•sinα
=-
;
(2)∵cos(α-
)=
,
∴sinα=-
,
又α是第三象限角,
∴cosα=-
,
∴f(α)=
;
(3)∵α=-1860°,
∴f(α)=f(-1860°)=-
=
=-
.
=sinαcosα•(-tanα)[-(-tanα)]•sinα
=-
| sin4α |
| cosα |
(2)∵cos(α-
| 3π |
| 2 |
| 1 |
| 5 |
∴sinα=-
| 1 |
| 5 |
又α是第三象限角,
∴cosα=-
2
| ||
| 5 |
∴f(α)=
| ||
| 1500 |
(3)∵α=-1860°,
∴f(α)=f(-1860°)=-
| sin4(-1860°) |
| cos(-1860°) |
(-
| ||||
|
| 9 |
| 8 |

练习册系列答案
相关题目
 ;(2)
;(2)
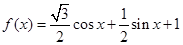
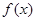 的值域和函数的单调递增区间;
的值域和函数的单调递增区间; 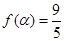 ,且
,且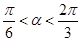 时,求
时,求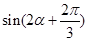 的值.
的值. ; (Ⅱ)
; (Ⅱ)
 ,则( )
,则( )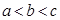
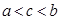

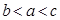
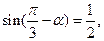 则
则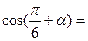 .
.