题目内容
已知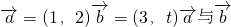 的夹角为锐角,则t的取值范围为________.
的夹角为锐角,则t的取值范围为________.
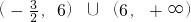
分析:先求出
 的值,由题意可得
的值,由题意可得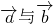 不共线,求得t≠6 ①,由cosθ=
不共线,求得t≠6 ①,由cosθ= >0 解得 t>-
>0 解得 t>- ②,结合①②确定出t的取值范围.
②,结合①②确定出t的取值范围.解答:由题意可得
 =(1,2)•(3,t)=3+2t.
=(1,2)•(3,t)=3+2t.由于
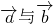 不共线,∴
不共线,∴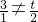 ,∴t≠6 ①.
,∴t≠6 ①.设
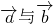 的夹角为θ,则θ 为锐角.
的夹角为θ,则θ 为锐角.由两个向量的夹角公式可得cosθ=
 >0.
>0.解得3+2t>0,故 t>-
 ②.
②.由①②可得t的取值范围为
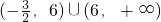 .
.故答案为:
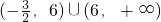 .
.点评:本题主要考查两个向量坐标形式的运算,两个向量夹角公式的应用,注意除去
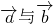 共线时的情况,这是解题的易错点.
共线时的情况,这是解题的易错点. 
练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
 夹角为锐角,则x的取值集合为
。
夹角为锐角,则x的取值集合为
。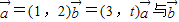 的夹角为锐角,则t的取值范围为 .
的夹角为锐角,则t的取值范围为 .