��Ŀ����
(��������12��)
����ʡ���������ξ��㣬ijͬѧ���ú�����������żҽ硢��������ɽ������¥���һ�Դ��5�����㣬���ղ����żҽ������Ʊ3�ţ�����������Ʊ2�ţ���ɽ������¥���һ�Դ������Ʊ��1�ţ��ִ��������ȡ5��.
�������ȡ��5����Ʊ��ǡ��3����ǡ��4������ĸ��ʣ�
��������ȡ��5����Ʊ��5�����㶼�м�10�֣�ǡ��4�������8�֣�ǡ��3�������6�֣���������.��![]() ��ʾ���õķ�������
��ʾ���õķ�������![]() �ķֲ��к���ѧ����.
�ķֲ��к���ѧ����.
��1��![]() ��2��������
��2��������
����:
���dz�ȡ��5����Ʊ�С�ǡ��3�����㡱Ϊ�¼�A����ǡ��4�����㡱Ϊ�¼�B.����ȡ��5����Ʊ��ǡ��3�����㣬������Ҫ��ȡ2���żҽ���Ʊ��
����![]() . ��2�֣�
. ��2�֣�
����ȡ��5����Ʊ��ǡ��4�����㣬������ֻ�ܳ�ȡ2���żҽ���Ʊ��
����![]() . ��5�֣�
. ��5�֣�
��Ϊ�¼�A��B���⣬����![]() .
.
�ʳ�ȡ��5����Ʊ��ǡ��3����ǡ��4������ĸ�����![]() . ��6�֣�
. ��6�֣�
������Ϊ5����Ʊ�����ٺ���2�����㣬��![]() �Ŀ���ȡֵΪ10��8��6��4. ��7�֣�
�Ŀ���ȡֵΪ10��8��6��4. ��7�֣�
����![]() ��
��![]() ��
��
![]() ��
��![]() . ��10�֣�
. ��10�֣�
����![]() �ķֲ���Ϊ
�ķֲ���Ϊ
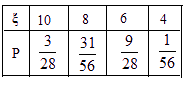 .
.
![]() . ��12�֣�
. ��12�֣�
