题目内容
9.设f(x)和g(x)是定义在R上的两个函数,其中f(x)是偶函数.对于任意实数x1,x2,不等式|f(x1)-f(x2)|≥|g(x1)-g(x2)|恒成立.(1)判断函数g(x)的奇偶性:
(2)若g(x+2)是奇函数,且g(0)=2015,求g(2016)的值.
分析 (1)令x2=-x1,不等式|f(x1)-f(x2)|≥|g(x1)-g(x2)|恒成立,结合f(x)是偶函数,可得函数g(x)是偶函数;
(2)判断g(x)是周期为8的周期函数,即可得出结论.
解答 解:(1)令x2=-x1,不等式|f(x1)-f(x2)|≥|g(x1)-g(x2)|恒成立,
∴不等式|f(x1)-f(-x1)|≥|g(x1)-g(-x1)|恒成立,
∵f(x)是偶函数,
∴f(-x1)=f(x1),
∴f(x1)-f(-x1)=0,
∴不等式0≥|g(x1)-g(-x1)|恒成立,又|g(x1)-g(-x1)|≥0,
∴g(x1)-g(-x1)=0,
∴g(-x1)=g(x1),
∴函数g(x)是偶函数;
(2)∵g(x+2)是奇函数,
∴g(-x+2)=-g(x+2),
∴g(-x)=-g(x+4),
∴g(x)=-g(x+4),
∴g(x+8)=g(x),
∴g(x)是周期为8的周期函数,
∵g(0)=2015,
∴g(2016)=g(8×252)=g(0)=2015.
点评 本题考查函数的周期性、奇偶性,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
5.用数学归纳法证明$\frac{1}{n+1}+\frac{1}{n+2}+…+\frac{1}{2n}>\frac{13}{24}$,由n=k到n=k+1左边需添加的项为( )
| A. | $\frac{1}{2(k+1)}$ | B. | $\frac{1}{2k+1}+\frac{1}{2k+2}-\frac{1}{k+1}$ | ||
| C. | $\frac{1}{2k+1}+\frac{1}{2k+2}+\frac{1}{k+1}$ | D. | $\frac{1}{2k+1}+\frac{1}{2k+2}$ |
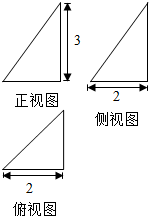 一个几何体的三视图是三个直角三角形,尺寸如图所示,求表面积.
一个几何体的三视图是三个直角三角形,尺寸如图所示,求表面积.