题目内容
19.定义$a⊕b=\left\{\begin{array}{l}ab(ab≥0)\\ \frac{a}{b}(ab<0)\end{array}\right.$,设函数f(x)=lnx⊕x,若数列{an}是公比大于0的等比数列,且a1008=1,f(a1)+f(a2)+f(a3)+…+f(a2015)+f(a2016)=a2016,则a2016=e.分析 f(x)=lnx⊕x=$\left\{\begin{array}{l}{xlnx,x≥1}\\{\frac{lnx}{x},0<x<1}\end{array}\right.$.由${a}_{1}{q}^{1007}$=a1008=1,q>0,可得a1>0.当q>1时,0<a1<1,可得数列{an}是单调递增数列,f(a1)+f(a2)+f(a3)+…+f(a2015)+f(a2016)=$\frac{ln{a}_{1}}{{a}_{1}}$+$\frac{ln{a}_{2}}{{a}_{2}}$+…+$\frac{ln{a}_{1008}}{{a}_{1008}}$+a1009lna1009+…+a2016lna2016=a2016,由于aka2016-k=${a}_{1008}^{2}$=1,(1≤k≤1007,k∈N*),可得$\frac{ln{a}_{k}}{{a}_{k}}$+a2016-kln(a2016-k)=0,于是可得:a2016lna2016=a2016,即可得出.当q<1时,0<a1<1,数列{an}是单调递减数列,同理可得.
解答 解:f(x)=lnx⊕x=$\left\{\begin{array}{l}{xlnx,x≥1}\\{\frac{lnx}{x},0<x<1}\end{array}\right.$.
由${a}_{1}{q}^{1007}$=a1008=1,q>0,
可得a1>0,
当q>1时,0<a1<1,∴数列{an}是单调递增数列,因此a1<a2<…<a1008=1<a1009<…<a2016,
∴f(a1)+f(a2)+f(a3)+…+f(a2015)+f(a2016)=$\frac{ln{a}_{1}}{{a}_{1}}$+$\frac{ln{a}_{2}}{{a}_{2}}$+…+$\frac{ln{a}_{1008}}{{a}_{1008}}$+a1009lna1009+…+a2016lna2016=a2016,(*)
∵aka2016-k=${a}_{1008}^{2}$=1,(1≤k≤1007,k∈N*),
∴$\frac{ln{a}_{k}}{{a}_{k}}$+a2016-kln(a2016-k)=0,
∴(*)化为:a2016lna2016=a2016,
解得a2016=e.
当q<1时,0<a1<1,∴数列{an}是单调递减数列,因此a1>a2>…>a1008=1>a1009>…>a2016,同理可得:a2016=e.
点评 本题考查了等差数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

| A. | 12≤Tn<16 | B. | 8≤Tn<16 | C. | 12≤Tn<$\frac{32}{3}$ | D. | 8≤Tn<$\frac{32}{3}$ |
| A. | 3个 | B. | 4个 | C. | 1个 | D. | 2个 |
 《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑,如图,在鳖臑PABC中,PA⊥平面ABC,AB⊥BC,且AP=AC=1,过A点分别作AE⊥PB于E、AF⊥PC于F,连接EF当△AEF的面积最大时,tan∠BPC的值是( )
《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑,如图,在鳖臑PABC中,PA⊥平面ABC,AB⊥BC,且AP=AC=1,过A点分别作AE⊥PB于E、AF⊥PC于F,连接EF当△AEF的面积最大时,tan∠BPC的值是( )| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
| A. | $\frac{18}{5},\frac{9}{10},-\frac{1}{2}$ | B. | $-\frac{18}{5},\frac{9}{10},-\frac{1}{2}$ | C. | $\frac{18}{5},-\frac{9}{10},-\frac{1}{2}$ | D. | $-\frac{18}{5},-\frac{9}{10},\frac{1}{2}$ |
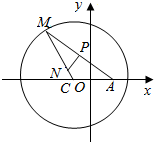 如图所示,已知圆(x+3)2+y2=100,定点A(3,0),M为圆C上一动点,点P在AM上,点N在CM上,且满足$\overrightarrow{AM}$=2$\overrightarrow{AP}$,$\overrightarrow{NP}$•$\overrightarrow{AM}$=0,点N的轨迹为曲线E.
如图所示,已知圆(x+3)2+y2=100,定点A(3,0),M为圆C上一动点,点P在AM上,点N在CM上,且满足$\overrightarrow{AM}$=2$\overrightarrow{AP}$,$\overrightarrow{NP}$•$\overrightarrow{AM}$=0,点N的轨迹为曲线E.