题目内容
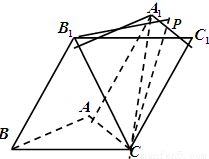
(本小题满分12分)如图,三棱柱 的各棱长均为2,侧面
的各棱长均为2,侧面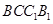
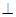 底面
底面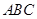 ,侧棱
,侧棱 与底面
与底面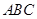 所成的角为
所成的角为 .
.
(1) 求直线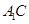 与底面
与底面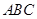 所成的角;
所成的角;
(2) 在线段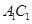 上是否存在点
上是否存在点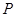 ,使得平面
,使得平面 平面
平面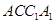 ?若存在,求出
?若存在,求出 的长;若不存在,请说明理由。
的长;若不存在,请说明理由。
【答案】
(1)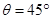 ;(2)
;(2)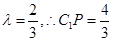 。
。
【解析】
试题分析:(1)根据题意建立空间直角坐标系,然后表示平面的法向量和直线的斜向量,进而利用向量的夹角公式得到线面角的求解。
(2)假设存在点满足题意,然后利用向量的垂直关系,得到点的坐标。
解:(1)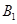 作
作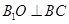 于
于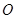 ,
,
∵侧面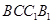
 平面
平面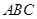 ,
,

则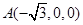 ,
,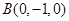 ,
,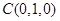 ,
,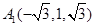 ,
,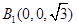 ,
,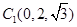
∴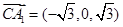 ,又底面
,又底面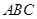 的法向量
的法向量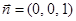 …4分
…4分
设直线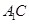 与底面
与底面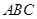 所成的角为
所成的角为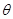 ,则
,则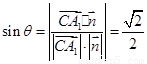 ,∴
,∴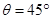
所以,直线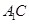 与底面
与底面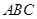 所成的角为
所成的角为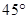 . …6分
. …6分
(2)设在线段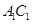 上存在点
上存在点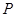 ,设
,设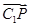 =
= ,
,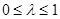 ,则
,则
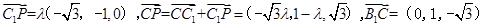 …7分
…7分
设平面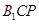 的法向量
的法向量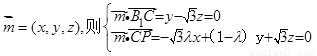
令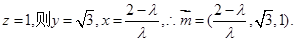 …9分
…9分
设平面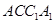 的法向量
的法向量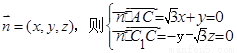
令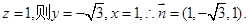 …10分
…10分
要使平面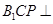 平面
平面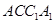 ,则
,则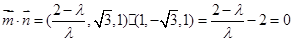
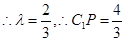 …12分
…12分
考点:本题主要是考查线面角的求解,以及面面垂直的探索性命题的运用。
点评:解决该试题的关键是合理的建立空间直角坐标系,正确的表示点的坐标,得到平面的法向量和斜向量,进而结合数量积的知识来证明垂直和求解角的问题。

练习册系列答案
相关题目