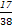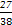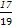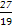题目内容
某市职教中心组织厨师技能大赛,大赛依次设基本功(初赛)、面点制作(复赛)、热菜烹制(决赛)三个轮次的比赛,已知某选手通过初赛、复赛、决赛的概率分别是 ,
, ,
, 且各轮次通过与否相互独立.
且各轮次通过与否相互独立.
(1)设该选手参赛的轮次为ξ,求ξ的分布列.
(2)对于(1)中的ξ,设“函数f(x)=3sin π(x∈R)是偶函数”为事件D,求事件D发生的概率.
π(x∈R)是偶函数”为事件D,求事件D发生的概率.
 ,
, ,
, 且各轮次通过与否相互独立.
且各轮次通过与否相互独立.(1)设该选手参赛的轮次为ξ,求ξ的分布列.
(2)对于(1)中的ξ,设“函数f(x)=3sin
 π(x∈R)是偶函数”为事件D,求事件D发生的概率.
π(x∈R)是偶函数”为事件D,求事件D发生的概率.(1) ξ的分布列为:
(2)
| ξ | 1 | 2 | 3 |
| P |  |  |  |

(1)ξ可能取值为1,2,3.
记“该选手通过初赛”为事件A,“该选手通过复赛”为事件B,
P(ξ=1)=P(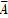 )=1-
)=1- =
= ,
,
P(ξ=2)=P(A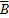 )=P(A)P(
)=P(A)P(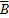 )=
)= ×(1-
×(1- )=
)= ,
,
P(ξ=3)=P(AB)=P(A)P(B)= ×
× =
= .
.
ξ的分布列为:
(2)当ξ=1时,
f(x)=3sin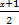 π=3sin(
π=3sin(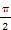 x+
x+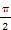 )
)
f(x)为偶函数;
当ξ=2时,
f(x)=3sin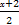 π=3sin(
π=3sin(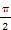 x+π)
x+π)
f(x)为奇函数;
当ξ=3时,
f(x)=3sin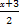 π=3sin(
π=3sin(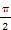 x+
x+ π)
π)
f(x)为偶函数;
∴事件D发生的概率是 .
.
记“该选手通过初赛”为事件A,“该选手通过复赛”为事件B,
P(ξ=1)=P(
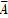 )=1-
)=1- =
= ,
,P(ξ=2)=P(A
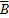 )=P(A)P(
)=P(A)P(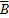 )=
)= ×(1-
×(1- )=
)= ,
,P(ξ=3)=P(AB)=P(A)P(B)=
 ×
× =
= .
.ξ的分布列为:
| ξ | 1 | 2 | 3 |
| P |  |  |  |
f(x)=3sin
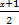 π=3sin(
π=3sin(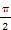 x+
x+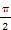 )
)f(x)为偶函数;
当ξ=2时,
f(x)=3sin
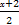 π=3sin(
π=3sin(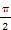 x+π)
x+π)f(x)为奇函数;
当ξ=3时,
f(x)=3sin
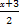 π=3sin(
π=3sin(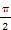 x+
x+ π)
π)f(x)为偶函数;
∴事件D发生的概率是
 .
.
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 ,将这10株树苗的高度依次输入按程序框图进行运算(如图),问输出的S大小为多少?并说明S的统计学意义;
,将这10株树苗的高度依次输入按程序框图进行运算(如图),问输出的S大小为多少?并说明S的统计学意义;
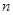 名女生中,任选3人参加比赛,已知在选出的3人中至少有1名女生的概率为
名女生中,任选3人参加比赛,已知在选出的3人中至少有1名女生的概率为 ,则
,则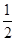 ,P(B)=
,P(B)= ,则出现奇数点或2点的概率为________.
,则出现奇数点或2点的概率为________.



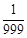
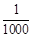
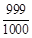
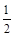
 )i,i=1,2,3,则a的值是( )
)i,i=1,2,3,则a的值是( )