题目内容
设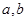 为实数,我们称
为实数,我们称 为有序实数对.类似地,设
为有序实数对.类似地,设 为集合,我们称
为集合,我们称 为有序三元组.如果集合
为有序三元组.如果集合 满足
满足 ,且
,且 ,则我们称有序三元组
,则我们称有序三元组 为最小相交(
为最小相交( 表示集合
表示集合 中的元素的个数).
中的元素的个数).
(Ⅰ)请写出一个最小相交的有序三元组,并说明理由;
(Ⅱ)由集合 的子集构成的所有有序三元组中,令
的子集构成的所有有序三元组中,令 为最小相交的有序三元组的个数,求
为最小相交的有序三元组的个数,求 的值.
的值.
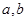 为实数,我们称
为实数,我们称 为有序实数对.类似地,设
为有序实数对.类似地,设 为集合,我们称
为集合,我们称 为有序三元组.如果集合
为有序三元组.如果集合 满足
满足 ,且
,且 ,则我们称有序三元组
,则我们称有序三元组 为最小相交(
为最小相交( 表示集合
表示集合 中的元素的个数).
中的元素的个数).(Ⅰ)请写出一个最小相交的有序三元组,并说明理由;
(Ⅱ)由集合
 的子集构成的所有有序三元组中,令
的子集构成的所有有序三元组中,令 为最小相交的有序三元组的个数,求
为最小相交的有序三元组的个数,求 的值.
的值.(Ⅰ)详见解析;(Ⅱ)7680.
试题分析:(Ⅰ)按条件写出即可;(Ⅱ)先排
 ,
,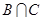 ,
,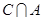 中的元素,再排其它位置的元素,根据乘法原理计算.
中的元素,再排其它位置的元素,根据乘法原理计算.试题解析:(Ⅰ)设
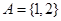 ,
,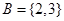 ,
,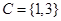 ,则
,则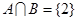 ,
,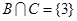 ,
,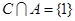 ,
, ,且
,且 .
.所以
 是一个最小相交的有序三元组. 4分
是一个最小相交的有序三元组. 4分(Ⅱ)令
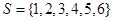 ,如果
,如果 是由
是由 的子集构成的最小相交的有序三元组,则存在两两不同的
的子集构成的最小相交的有序三元组,则存在两两不同的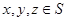 ,使得
,使得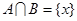 ,
,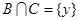 ,
,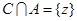 (如图),要确定
(如图),要确定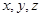 共有
共有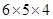 种方法;对
种方法;对 中剩下的3个元素,每个元素有4种分配方式,即它属于集合
中剩下的3个元素,每个元素有4种分配方式,即它属于集合 中的某一个或不属于任何一个,则有
中的某一个或不属于任何一个,则有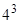 种确定方法.
种确定方法. 所以最小相交的有序三元组
 的个数
的个数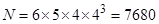 . 10分
. 10分

练习册系列答案
相关题目
 ,
, ),且EX=3,DX=1,则P(-1<X<1)="( " )
),且EX=3,DX=1,则P(-1<X<1)="( " )
 个人报名参加
个人报名参加 项体育比赛,每个人限报一项,则不同的报名方法的种数有( )
项体育比赛,每个人限报一项,则不同的报名方法的种数有( )


