题目内容
设 a∈R,若x>0时均有 ,则a=
,则a=
 ,则a=
,则a= 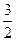
当a=1时,原不等式为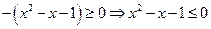 ,显然对x>0不等式不恒成立,故a=1舍去;
,显然对x>0不等式不恒成立,故a=1舍去;
当a<1时,对x>0,(a-1)x-1<0恒成立,所以原不等式等价于x2-ax-1≤0(x>0).取a=0,x=2知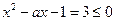 不成立,故a<1舍去;
不成立,故a<1舍去;
当a>1时,原不等式为(x-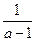 )(
)(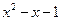 )≥0.因为判别式
)≥0.因为判别式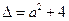 >0,所以方程
>0,所以方程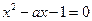 有两个根,由于
有两个根,由于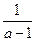 >0,所以根椐数轴标根法知,若x>0时均有(x-
>0,所以根椐数轴标根法知,若x>0时均有(x-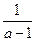 )(
)(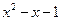 )≥0,则
)≥0,则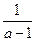 必是方程
必是方程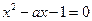 的一个根,且另一根为1-a<0.把1-a代入方程
的一个根,且另一根为1-a<0.把1-a代入方程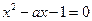 得a=0(舍)或a=
得a=0(舍)或a=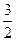 .检验知a=
.检验知a=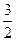 满足题意.
满足题意.
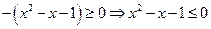 ,显然对x>0不等式不恒成立,故a=1舍去;
,显然对x>0不等式不恒成立,故a=1舍去;当a<1时,对x>0,(a-1)x-1<0恒成立,所以原不等式等价于x2-ax-1≤0(x>0).取a=0,x=2知
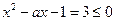 不成立,故a<1舍去;
不成立,故a<1舍去;当a>1时,原不等式为(x-
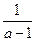 )(
)(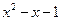 )≥0.因为判别式
)≥0.因为判别式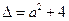 >0,所以方程
>0,所以方程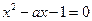 有两个根,由于
有两个根,由于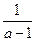 >0,所以根椐数轴标根法知,若x>0时均有(x-
>0,所以根椐数轴标根法知,若x>0时均有(x-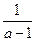 )(
)(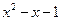 )≥0,则
)≥0,则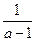 必是方程
必是方程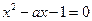 的一个根,且另一根为1-a<0.把1-a代入方程
的一个根,且另一根为1-a<0.把1-a代入方程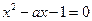 得a=0(舍)或a=
得a=0(舍)或a=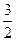 .检验知a=
.检验知a=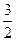 满足题意.
满足题意.
练习册系列答案
相关题目
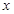 的不等式
的不等式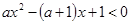
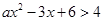 的解集为
的解集为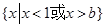 .
.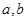 的值;
的值;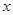 不等式:
不等式: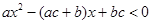 .
.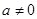 ,函数
,函数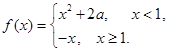 若
若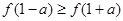 ,则实数
,则实数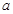 的取值范围是( )
的取值范围是( )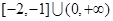
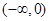
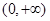
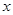 的不等式
的不等式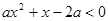 的解集中有且仅有4个整数解,则实数
的解集中有且仅有4个整数解,则实数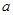 的取值范围是 .
的取值范围是 .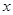 的不等式
的不等式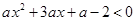 的解集为
的解集为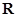 ,则实数
,则实数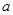 的取值范围 .
的取值范围 .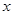 的不等式
的不等式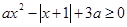 的解集为
的解集为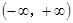 ,则实数
,则实数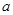 的取值范围是________.
的取值范围是________. 的解集是
的解集是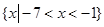 ,那么
,那么 的值是 ( )
的值是 ( )