��Ŀ����
����Ŀ��ij���мƻ�����ij��ʳƷ��������ס��������̼ҽ�������10�죮�����̼��ṩ�ķ����������£����̼�ÿ��̶�����60Ԫ����ÿ����һ��ʳƷ�̼��ٷ���3Ԫ�����̼��̶�����������30�����ڣ���30������ʳƷ��ÿ��ʳƷ�̼ҷ���5Ԫ������30���IJ���ÿ������8Ԫ����ͳ�ƣ������̼ҵ����������Ҷͼ���£�
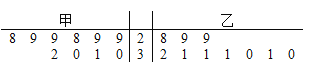
��1���ִӼ��̼�������10���г�ȡ���죬�����������������С��30�ĸ��ʣ�
��2������Ƶ���������ʣ��ش��������⣺
�� ���̼��ҵ��շ�����ΪX����λ��Ԫ������X�ķֲ��к���ѧ������
�� �������ڼס��������̼���ѡ��һ�ҳ������ۣ����������ƽ��������ĽǶȿ��ǣ���������ѧ��ͳ��ѧ֪ʶΪ��������ѡ��˵�����ɣ�
���𰸡���1��![]() ����2��������������������.
����2��������������������.
�������������������1��������֪ʶ�����ùŵ�����ʹ�ʽ�������������������С��![]() �ĸ��ʣ���2����
�ĸ��ʣ���2����![]() �����п���ȡֵΪ��
�����п���ȡֵΪ�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() �����ݹŵ�����ʹ�ʽ������������������Ӧ�ĸ��ʣ��Ӷ��ɵ�
�����ݹŵ�����ʹ�ʽ������������������Ӧ�ĸ��ʣ��Ӷ��ɵ�![]() �ķֲ��У������ɵ�����ֵ������������̼ҵ���ƽ�����������Ӷ��ɵü��̼ҵ���ƽ����������ɢٵó����̼ҵ���ƽ��������ȽϷ�����Ĵ�С�ɵý���.
�ķֲ��У������ɵ�����ֵ������������̼ҵ���ƽ�����������Ӷ��ɵü��̼ҵ���ƽ����������ɢٵó����̼ҵ���ƽ��������ȽϷ�����Ĵ�С�ɵý���.
�����������1��������ȡ��������������С��30��Ϊ�¼�A��
��P(A)= ![]() =
=![]() ��
��
��2�������̼ҵ���������Ϊa����
��a=28ʱ��X=28��5=140��
��a=29ʱ��X=29��5=145��
��a=30ʱ��X=30��5=150��
��a=31ʱ��X=30��5+1��8=158��
��a=32ʱ��X=30��5+2��8=166��
����X�����п���ȡֵΪ��140��145��150��158��166��
����X�ķֲ���Ϊ
X | 140 | 145 | 150 | 158 | 166 |
P |
|
|
|
|
|
����EX=140��![]() +145��
+145��![]() +150��
+150��![]() +158��
+158��![]() +166��
+166��![]() =152.8.
=152.8.
�������⣬���̼ҵ���ƽ��������Ϊ��28��0.2+29��0.4+30��0.2+31��0.1+32��0.1=29.5
���Լ��̼ҵ���ƽ��������Ϊ��60+29.5��3=148.5Ԫ��
�ɢٵ����̼ҵ���ƽ��������Ϊ152.8Ԫ����148.5Ԫ����
�����Ƽ��ó���ѡ�����̼ҳ������ۣ�

����Ŀ���±���20�����Һ͵����Ķ�����̼�ŷ��������˾�������̼�ŷ���.
���Һ͵��� | �ŷ�����/ǧ�� | �˾��ŷ���/�� | ���Һ͵��� | �ŷ�����/ǧ�� | �˾��ŷ���/�� | |
A | 10330000 | 7.4 | K | 480000 | 2.0 | |
B | 5300000 | 16.6 | L | 480000 | 7.5 | |
C | 3740000 | 7.3 | M | 470000 | 3.9 | |
D | 2070000 | 1.7 | N | 410000 | 5.3 | |
E | 1800000 | 12.6 | O | 390000 | 16.9 | |
F | 1360000 | 10.7 | P | 390000 | 6.4 | |
G | 840000 | 10.2 | Q | 370000 | 5.7 | |
H | 630000 | 12.7 | R | 330000 | 6.2 | |
I | 550000 | 15.7 | S | 320000 | 6.2 | |
J | 510000 | 2.6 | T | 490000 | 16.6 |
��1����20�����Һ͵����˾�������̼�ŷ�������λ���Ƕ��٣�
��2�������20�����Һ͵����������ҳ�������̼�ŷ��������ٵ�ǰ15%�Ĺ��Һ͵���.
����Ŀ��Ϊ�˽����Ƕԡ��ӳ������������ߡ���̬�ȣ�ij���Ŵ�������![]() �굽
�굽![]() �����Ⱥ�����������
�����Ⱥ�����������![]() �ˣ����õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ������
�ˣ����õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ������![]() ���в�֧�֡��ӳ������������ߡ��������������ͳ�ƽ����ͼ��ʾ��
���в�֧�֡��ӳ������������ߡ��������������ͳ�ƽ����ͼ��ʾ��

���� | ��֧�֡��ӳ������������ߡ������� |
|
|
|
|
|
|
|
|
|
|
��1����Ƶ�ʷֲ�ֱ��ͼ��������![]() �������ƽ������
�������ƽ������
��2����������ͳ��������д�����![]() ���������ݴ˱����ܷ��ڷ�����ĸ��ʲ�����
���������ݴ˱����ܷ��ڷ�����ĸ��ʲ�����![]() ��ǰ���£���Ϊ��
��ǰ���£���Ϊ��![]() ��Ϊ�ֽ��IJ�ͬ��Ⱥ�ԡ��ӳ������������ߡ���̬�ȴ��ڲ��죿
��Ϊ�ֽ��IJ�ͬ��Ⱥ�ԡ��ӳ������������ߡ���̬�ȴ��ڲ��죿
45������ | 45������ | �ܼ� | |
��֧�� | |||
֧�� | |||
�ܼ� |
����![]()
�ο����ݣ�
|
|
|
|
|
|
|
|
|
|