题目内容
3．设函数f（x）=x4-2x2+3．（1）求曲线f（x）=x4-2x2+3在点（2，11）处的切线方程；
（2）求函数f（x）的单调区间．
分析 （1）求导数，确定切线的斜率，即可求曲线f（x）=x4-2x2+3在点（2，11）处的切线方程；
（2）利用导数的正负求函数f（x）的单调区间．
解答 解：（1）函数f（x）=x4-2x2+3明显在整个定义域内可导，则其导数f'（x）=4x3-4x
∴f'（2）=24
∴函数的切线方程为y-11=24（x-2），即y=24x-37；
（2）f'（x）=4x3-4x＞0，可得-1＜x＜0或x＞1，f'（x）=4x3-4x＞0，可得x＜-1或0＜x＜1
∴函数f（x）的单调增区间是（-1，0），（1，+∞）；单调减区间是（-∞，-1），（0，1）．
点评 本题考查导数知识的综合运用，考查导数的几何意义，单调性，正确求导是关键．
练习册系列答案
步步高达标卷系列答案
相关题目
11．某高中学校共有学生2000名，各年级男、女人数如下表：
已知从全校学生中随机抽取1名，抽到高二年级女生的概率是0.19．
（1）求x的值；
（2）已知y≥245，z≥245，且在高三年级任意抽取一人，抽到男生的概率大于抽到女生的概率，试写出y、z所有取值．
| 高一年级 | 高二年级 | 高三年级 | |
| 女生 | 373 | X | Y |
| 男生 | 377 | 370 | z |
（1）求x的值；
（2）已知y≥245，z≥245，且在高三年级任意抽取一人，抽到男生的概率大于抽到女生的概率，试写出y、z所有取值．
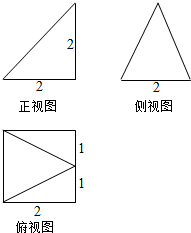如图是一个几何体的三视图，根据图中所给的数据，求这个几何体的表面积和体积．