题目内容
(理)设x1、x2(x1≠x2)是函数f(x)=ax3+bx2-a2x(a>0)的两个极值点.(1)若x1=-1,x2=2,求函数f(x)的解析式;
(2)若|x1|+|x2|=![]() ,求b的最大值;
,求b的最大值;
(3)若x1<x<x2,且x2=a,函数g(x)=f′(x)-a(x-x1),求证:|g(x)|≤![]() a(3a+2)2.
a(3a+2)2.
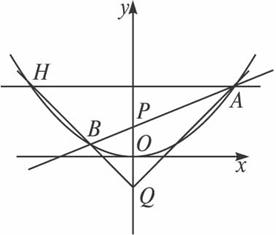
(文)如图,N为圆x2+(y-2)2=4上的点,OM为直径,连结MN并延长交x轴于点C,过C引直线垂直于x轴,且与弦ON的延长线交于点D.

(1)已知点N(![]() ,1),求点D的坐标;
,1),求点D的坐标;
(2)若点N沿着圆周运动,求点D的轨迹E的方程;
(3)设P(0,a)(a>0),Q是点P关于原点的对称点,直线l过点P交曲线E于A、B两点,点H在射线QB上,且AH⊥PQ,求证:不论l绕点P怎样转动,恒有![]() .
.
答案:(理)解:f′(x)=3ax2+2bx-a2(a>0).
(1)∵x1=-1,x2=2是函数f(x)的两个极值点,∴f′(-1)=0,f′(2)=0.∴3a-2b-a2=0,12a+4b-a2=0,解得a=6,b=-9.∴f(x)=6x3-9x2-36x.
(2)∵x1、x2是f(x)的两个极值点,∴f′(x1)=f′(x2)=0.∴x1、x2是方程3ax2+2bx-a2=0的两根.∵Δ=4b2+12a3,∴Δ>0对一切a>0,b∈R恒成立.x1+x2=![]() ,x1+x2=
,x1+x2=![]() ,∵a>0,∴x1·x2<0.∴|x1|+|x2|=|x1-x2|=
,∵a>0,∴x1·x2<0.∴|x1|+|x2|=|x1-x2|=![]() .
.
由|x1|+|x2|=22,得![]() ,∴b2=3a2(6-a).∵b2≥0,∴3a2(6-a)≥0.∴0<a≤6.
,∴b2=3a2(6-a).∵b2≥0,∴3a2(6-a)≥0.∴0<a≤6.
令h(a)=3a2(6-a),则h′(a)=-9a2+36a.
当0<a<4时,h′(a)>0,∴h(a)在(0,4)上是增函数;
当4<a<6时,h′(a)<0,∴h(a)在(4,6)上是减函数.
∴当a=4时,h(a)有极大值为96.∴h(a)在(0,6]上的最大值是96.∴b的最大值是![]() .
.
(3)∵x1、x2是方程f′(x)=0的两根,∴f′(x)=3a(x-x1)(x-x2).
∴|g(x)|=3a|x-x1|·|x-x2-![]() |≤3a
|≤3a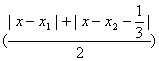 2.
2.
∵x1<x<x2,∴x-x1>0,x-x2<0.∴|g(x)|≤![]() [(x-x1)-(x-x2-
[(x-x1)-(x-x2-![]() )]2=
)]2=![]() (x2-x1+
(x2-x1+![]() )2.
)2.
∵x1·x2=![]() ,x2=a,∴x1=-
,x2=a,∴x1=-![]() .∴|g(x)|≤
.∴|g(x)|≤![]() ·(a+
·(a+![]() +
+![]() )2=
)2=![]() a(3a+2)2.
a(3a+2)2.
(文)(1)∵M(0,4)、N(![]() ,1),∴MN所在直线的方程为
,1),∴MN所在直线的方程为![]() ,
,
即y=![]() x+4.令y=0,得x
x+4.令y=0,得x![]() ,∴C(
,∴C(![]() ,0).又ON所在直线方程为y=
,0).又ON所在直线方程为y=![]() x,
x,
由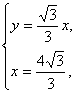 得y=
得y=![]() .∴点D坐标为(
.∴点D坐标为(![]() ,
,![]() ).
).
(2)∵M(0,4),O(0,0),设D(x,y),N(x1,y1),∴C(x,0).

过N作NK⊥OC于K,则NK∥CD∥OM,∴![]() ,即
,即![]() .①
.①
![]() ,即
,即![]() .②
.②
由①②,得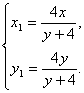 ∵点N在圆x2+(y-2)2=4上,
∵点N在圆x2+(y-2)2=4上,
∴x12+(y1-2)2=4,即(![]() )2+(
)2+(![]() -2)2=4.整理,得x2=4y.
-2)2=4.整理,得x2=4y.
(3)∵直线l过点P(0,a)且交曲线x2=4y于A、B两点,故可设直线l的方程为y=kx+a,设A(x1,y1),B(x2,y2).
由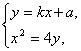 得x2-4kx-4a=0,∴x1x2=-4a.
得x2-4kx-4a=0,∴x1x2=-4a.
设P分![]() 的比为λ,则
的比为λ,则![]() ,且
,且![]() =0,∴λ=
=0,∴λ=![]() .
.
又∵Q(0,-a),∴![]() =(0,2a),
=(0,2a),![]() =(x2,y2+a),
=(x2,y2+a),![]() =(x1,y1+a).
=(x1,y1+a).
∵点H在射线QB上,设![]() =m·
=m·![]() ,则
,则
![]() =m·
=m·![]() =(mx2-x1,my2-y1-(1-m)a),
=(mx2-x1,my2-y1-(1-m)a),
∵AH⊥PQ,∴![]() =0,即2a[my2-y1-(1-m)a]=0.∵a≠0,y1=
=0,即2a[my2-y1-(1-m)a]=0.∵a≠0,y1=![]() x12,y2=
x12,y2=![]() x22,
x22,
m·![]() -(1-m)a=0,m·
-(1-m)a=0,m·![]() +
+![]() x1x2=0,m·x22-x12+(1-m)x1x2=0,
x1x2=0,m·x22-x12+(1-m)x1x2=0,
(![]() )2+(m-1)
)2+(m-1)![]() -m=0,λ2-(m-1)λ-m=0,(λ-m)(λ+1)=0,
-m=0,λ2-(m-1)λ-m=0,(λ-m)(λ+1)=0,
∵λ≠-1,∴λ=m.依题意,得λ>0,m>0,
∴λ=![]() ,m=
,m=![]() .∴
.∴![]() =
=![]() .
.
