题目内容
15、（理）设定义域为R的函数f（x）=|x2-2x-3|，若关于x的方程f2（x）+bf（x）+c=0有且只有5个不同的实数根x1，x2，x3，x4，x5，则x1+x2+x3+x4+x5=
5
．分析：先根据一元二次方程根的情况可判断f（x）=4一定是三个解，再根据f（x）的图象可知f（x）＞4或f（x）=0有两解，根据图象的对称性可知所求．
解答：解：对于f2（x）+bf（x）+c=0来说，f（x）最多只有2解，
又f（x）=|x2-2x-3|，x最多四解．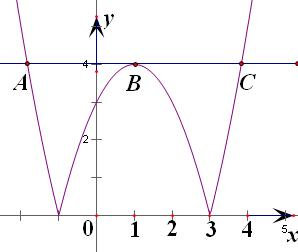
而题目要求5解，即可推断f（x）=4为三解！
算出x2=1，x1+x3=2；
f（x）＞4或f（x）=0有两解；
x4+x5=2
所以：x1+x2+x3+x4+x5=2+2+1=5；
故答案为：5．
又f（x）=|x2-2x-3|，x最多四解．
而题目要求5解，即可推断f（x）=4为三解！
算出x2=1，x1+x3=2；
f（x）＞4或f（x）=0有两解；
x4+x5=2
所以：x1+x2+x3+x4+x5=2+2+1=5；
故答案为：5．
点评：本题主要考查一元二次方程根的情况和含有绝对值的函数的解法，考查基础知识的综合运用能力，以及数形结合的思想，属于中档题．
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
，则关于
的方程
有7个不同实数解的充要条件是（ ）
且
B．
且
C．
D．
且