题目内容
已知函数f(x)=ax+b,当x∈[a1,b1]时,值域为[a2,b2],当x∈[a2,b2]时,值域为[a3,b3],…,当x∈[an-1,bn-1]时,值域为[an,bn],….其中a、b为常数,a1=0,b1=1.(1)若a=1,求数列{an}与数列{bn}的通项公式;
(2)若a>0,a≠1,要使数列{bn}是公比不为1的等比数列,求b的值;
(3)若a>0,设数列{an}与{bn}的前n项和分别为Sn和Tn,求(T1+T2+…+T2 007)-(S1+S2+…+S2 007)的值.
解:(1)∵a=1>0,∴f(x)=ax+b在R上为增函数,
∴an=a·an-1+b=an-1+b,bn=bn-1+b(n≥2),
∴数列{an},{bn}都是公差为b的等差数列.
又a1=0,b1=1,
∴an=(n-1)b,bn=1+(n-1)b(n≥2).
(2)∵a>0,bn=abn-1+b,∴![]() ,
,
由{bn}是等比数列知![]() 为常数.
为常数.
又∵{bn}是公比不为1的等比数列,则bn-1不为常数,
∴必有b=0.
(3)∵a>0,an=a·an-1+b,bn=a·bn-1+b,两式相减得bn-an=a(bn-1-an-1),
∴bn-an=(b1-a1)·an-1=an-1,
∴Tn-Sn=(b1-a1)+(b2-a2)+…+(bn-an)=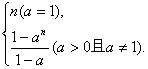
∴(T1+T2+…+T2 007)-(S1+S2+…+S2 007)
=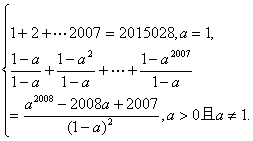

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
已知函数f(x)=a-
,若f(x)为奇函数,则a=( )
| 1 |
| 2x+1 |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |