题目内容
某单位决定对本单位职工实行年医疗费用报销制度,拟制定年医疗总费用在2万元至10万元(包括2万元和10万元)的报销方案,该方案要求同时具备下列三个条件:①报销的医疗费用y(万元)随医疗总费用x(万元)增加而增加;②报销的医疗费用不得低于医疗总费用的50%;③报销的医疗费用不得超过8万元.
(1)请你分析该单位能否采用函数模型y=0.05(x2+4x+8)作为报销方案;
(2)若该单位决定采用函数模型y=x-2lnx+a(a为常数)作为报销方案,请你确定整数a的值.(参考数据:ln2≈0.69,ln10≈2.3)
(1)请你分析该单位能否采用函数模型y=0.05(x2+4x+8)作为报销方案;
(2)若该单位决定采用函数模型y=x-2lnx+a(a为常数)作为报销方案,请你确定整数a的值.(参考数据:ln2≈0.69,ln10≈2.3)
(1)不符合(2)a的值为1.
审题引导:正确理解三个条件:①要求模型函数在[2,10]上是增函数;②要满足y≥ 恒成立;③要满足y的最大值小于8.
恒成立;③要满足y的最大值小于8.
规范解答:解:(1)函数y=0.05(x2+4x+8)在[2,10]上是增函数,满足条件①,(2分)
当x=10时,y有最大值7.4万元,小于8万元,满足条件③.(4分)
但当x=3时,y=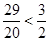 ,即y≥
,即y≥ 不恒成立,不满足条件②,故该函数模型不符合该单位报销方案.(6分)
不恒成立,不满足条件②,故该函数模型不符合该单位报销方案.(6分)
(2)对于函数模型y=x-2lnx+a,设f(x)=x-2lnx+a,则f′(x)=1- =
= ≥0.∴f(x)在[2,10]上是增函数,满足条件①.由条件②,得x-2lnx+a≥
≥0.∴f(x)在[2,10]上是增函数,满足条件①.由条件②,得x-2lnx+a≥ ,即a≥2lnx-
,即a≥2lnx- 在x∈[2,10]上恒成立,令g(x)=2lnx-
在x∈[2,10]上恒成立,令g(x)=2lnx- ,则g′(x)=
,则g′(x)= -
- =
= ,由g′(x)>0得0<x<4,∴g(x)在(0,4)上是增函数,在(4,10)上是减函数.
,由g′(x)>0得0<x<4,∴g(x)在(0,4)上是增函数,在(4,10)上是减函数.
∴a≥g(4)=2ln4-2=4ln2-2.(10分)
由条件③,得f(10)=10-2ln10+a≤8,解得a≤2ln10-2.
另一方面,由x-2lnx+a≤x,得a≤2lnx在x∈[2,10]上恒成立,∴a≤2ln2.(12分)
综上所述,a的取值范围为[4ln2-2,2ln2],
∴满足条件的整数a的值为1.(14分)
 恒成立;③要满足y的最大值小于8.
恒成立;③要满足y的最大值小于8.规范解答:解:(1)函数y=0.05(x2+4x+8)在[2,10]上是增函数,满足条件①,(2分)
当x=10时,y有最大值7.4万元,小于8万元,满足条件③.(4分)
但当x=3时,y=
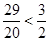 ,即y≥
,即y≥ 不恒成立,不满足条件②,故该函数模型不符合该单位报销方案.(6分)
不恒成立,不满足条件②,故该函数模型不符合该单位报销方案.(6分)(2)对于函数模型y=x-2lnx+a,设f(x)=x-2lnx+a,则f′(x)=1-
 =
= ≥0.∴f(x)在[2,10]上是增函数,满足条件①.由条件②,得x-2lnx+a≥
≥0.∴f(x)在[2,10]上是增函数,满足条件①.由条件②,得x-2lnx+a≥ ,即a≥2lnx-
,即a≥2lnx- 在x∈[2,10]上恒成立,令g(x)=2lnx-
在x∈[2,10]上恒成立,令g(x)=2lnx- ,则g′(x)=
,则g′(x)= -
- =
= ,由g′(x)>0得0<x<4,∴g(x)在(0,4)上是增函数,在(4,10)上是减函数.
,由g′(x)>0得0<x<4,∴g(x)在(0,4)上是增函数,在(4,10)上是减函数.∴a≥g(4)=2ln4-2=4ln2-2.(10分)
由条件③,得f(10)=10-2ln10+a≤8,解得a≤2ln10-2.
另一方面,由x-2lnx+a≤x,得a≤2lnx在x∈[2,10]上恒成立,∴a≤2ln2.(12分)
综上所述,a的取值范围为[4ln2-2,2ln2],
∴满足条件的整数a的值为1.(14分)

练习册系列答案
相关题目
 (单位:元)与上市时间
(单位:元)与上市时间 (单位:天)的数据如下:
(单位:天)的数据如下: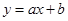 ;②
;② ;③
;③ .
.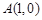 ,点
,点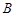 在曲线
在曲线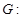
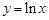 上,若线段
上,若线段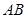 与曲线
与曲线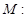
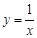 相交且交点恰为线段
相交且交点恰为线段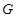 关于曲线
关于曲线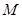 的一个关联点.那么曲线
的一个关联点.那么曲线 上的函数
上的函数 满足:对于任意的
满足:对于任意的 ,都有
,都有 ,且
,且 时,有
时,有 ,
,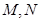 ,则
,则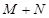 的值为( )
的值为( ) ,x∈A,y∈B,满足条件的对应法则f构成从集合A到集合B的函数;
,x∈A,y∈B,满足条件的对应法则f构成从集合A到集合B的函数; 与
与
 与
与
 与
与
 与
与
 (a<0)的定义域为D,若所有点(s,f(t))(s、t∈D)构成一个正方形区域,则a的值为________.
(a<0)的定义域为D,若所有点(s,f(t))(s、t∈D)构成一个正方形区域,则a的值为________.