题目内容
设等比数列{an}前n项和为Sn,若S3+S6=2S9.(Ⅰ)求数列的公比q;
(Ⅱ)求证:2S3,S6,S12-S6成等比数列.
【答案】分析:(Ⅰ)分公比等于1,验证数列是否成立;公比不等于1,利用前n项和公式求出公比,即可;
(Ⅱ)通过公比,推出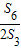 =
=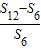 ,即可证明数列是等比数列.
,即可证明数列是等比数列.
解答:解 (Ⅰ)当q=1时,S3+S6=9a1,2S9=18a1.因为a1≠0,所以S3+S6≠2S9,由题设q≠1.从而由S3+S6=2S9得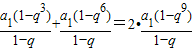 ,化简得2q9-q6-q3=0,
,化简得2q9-q6-q3=0,
因为q≠0,所以2q6-q3-1=0,即(2q3+1)(q3-1)=0.又q≠1,所以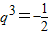 ,
,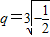 .
.
(Ⅱ)由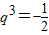 得
得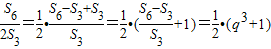 =
=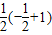 =
= ;
;
又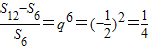 ,所以
,所以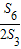 =
=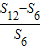 ,从而2S3,S6,S12-S6成等比数列.
,从而2S3,S6,S12-S6成等比数列.
点评:本题是中档题,考查数列的基本性质,注意等比数列公比的讨论,等比数列的证明,考查计算能力,常考题型.
(Ⅱ)通过公比,推出
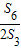 =
=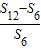 ,即可证明数列是等比数列.
,即可证明数列是等比数列.解答:解 (Ⅰ)当q=1时,S3+S6=9a1,2S9=18a1.因为a1≠0,所以S3+S6≠2S9,由题设q≠1.从而由S3+S6=2S9得
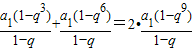 ,化简得2q9-q6-q3=0,
,化简得2q9-q6-q3=0,因为q≠0,所以2q6-q3-1=0,即(2q3+1)(q3-1)=0.又q≠1,所以
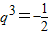 ,
,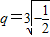 .
.(Ⅱ)由
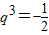 得
得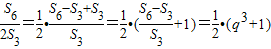 =
=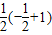 =
= ;
;又
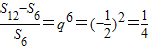 ,所以
,所以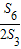 =
=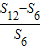 ,从而2S3,S6,S12-S6成等比数列.
,从而2S3,S6,S12-S6成等比数列.点评:本题是中档题,考查数列的基本性质,注意等比数列公比的讨论,等比数列的证明,考查计算能力,常考题型.

练习册系列答案
相关题目