题目内容
设U=R,集合A={x|x2+3x+2=0},B={x|x2+(m+1)x+m=0},若(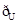 A)∩B=?,求m的值.
A)∩B=?,求m的值.
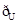 A)∩B=?,求m的值.
A)∩B=?,求m的值.m=1或2
方法一:A={-2,-1},
由(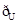 A)∩B=?得B⊆A,
A)∩B=?得B⊆A,
∵方程x2+(m+1)x+m=0的判别式:
Δ=(m+1)2-4m=(m-1)2≥0,∴B≠?,
∴B={-1}或B={-2}或B={-1,-2}.
①若B={-1},则m=1;
②若B={-2},则应有-(m+1)=(-2)+(-2)=-4且m=(-2)·(-2)=4,这两式不能同时成立,
∴B≠{-2};
③若B={-1,-2},则应有-(m+1)=(-1)+(-2)=-3且m=(-1)·(-2)=2,由这两式得m=2.
经检验知m=1和m=2符合条件.∴m=1或2.
方法二:本题集合B中的方程的根是x1=-1,x2=-m.
当-m≠-1时集合B={-1,-m},此时只能A=B,即m=2;当-m=-1时集合B={-1},此时集合B是集合A的真子集,也符合要求.∴m=1或2.
由(
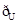 A)∩B=?得B⊆A,
A)∩B=?得B⊆A,∵方程x2+(m+1)x+m=0的判别式:
Δ=(m+1)2-4m=(m-1)2≥0,∴B≠?,
∴B={-1}或B={-2}或B={-1,-2}.
①若B={-1},则m=1;
②若B={-2},则应有-(m+1)=(-2)+(-2)=-4且m=(-2)·(-2)=4,这两式不能同时成立,
∴B≠{-2};
③若B={-1,-2},则应有-(m+1)=(-1)+(-2)=-3且m=(-1)·(-2)=2,由这两式得m=2.
经检验知m=1和m=2符合条件.∴m=1或2.
方法二:本题集合B中的方程的根是x1=-1,x2=-m.
当-m≠-1时集合B={-1,-m},此时只能A=B,即m=2;当-m=-1时集合B={-1},此时集合B是集合A的真子集,也符合要求.∴m=1或2.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,集合
,集合 .
. ;
; ,若
,若 ,求实数
,求实数 的取值范围.
的取值范围. },N={x|y=log2(x-2x2)},则
},N={x|y=log2(x-2x2)},则 (M∩N)=( )
(M∩N)=( ) ,
, )
)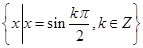 ,B={x||x-1|≤1},则A∩B=( ).
,B={x||x-1|≤1},则A∩B=( ). 则
则 ( )
( )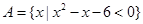 ,
,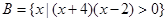 ,则
,则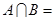 _ _.
_ _.