题目内容
(本小题满分14分)
设函数
(I)求函数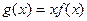 在区间[0,1]上的最小值;
在区间[0,1]上的最小值;
(II)当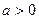 时,记曲线
时,记曲线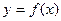 在点
在点 处的切线为
处的切线为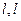 与x轴交于点
与x轴交于点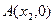 ,求证:
,求证: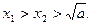
设函数

(I)求函数
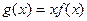 在区间[0,1]上的最小值;
在区间[0,1]上的最小值;(II)当
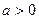 时,记曲线
时,记曲线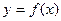 在点
在点 处的切线为
处的切线为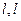 与x轴交于点
与x轴交于点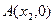 ,求证:
,求证: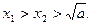
(1)1-a(2)略
(I)解: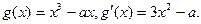 ………………2分
………………2分
当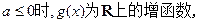
所以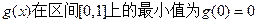 ; ………………4分
; ………………4分
当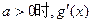 的变化情况如下表:
的变化情况如下表:
所以,函数
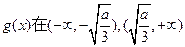 上单调递增,
上单调递增,
在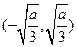 上单调递减。 ………………6分
上单调递减。 ………………6分
当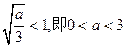 时,
时,
 ………………7分
………………7分
当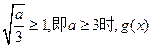 在区间[0,1]上的最小值为
在区间[0,1]上的最小值为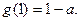 …………8分
…………8分
综上,当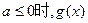 在区间[0,1]上的最小值为
在区间[0,1]上的最小值为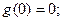
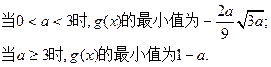
(II)证明:曲线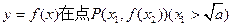 处的切线方程为
处的切线方程为
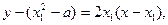
令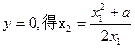 , ………………10分
, ………………10分
所以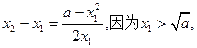
所以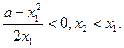 ………………11分
………………11分
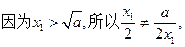
所以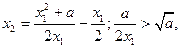 ………………13分
………………13分
所以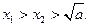 ………………14分
………………14分
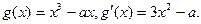 ………………2分
………………2分当
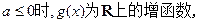
所以
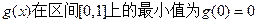 ; ………………4分
; ………………4分当
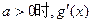 的变化情况如下表:
的变化情况如下表: | 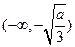 | 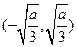 | 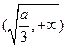 |
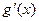 | + | — | + |

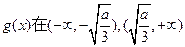 上单调递增,
上单调递增,在
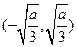 上单调递减。 ………………6分
上单调递减。 ………………6分当
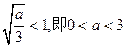 时,
时, ………………7分
………………7分当
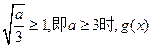 在区间[0,1]上的最小值为
在区间[0,1]上的最小值为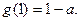 …………8分
…………8分综上,当
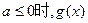 在区间[0,1]上的最小值为
在区间[0,1]上的最小值为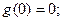
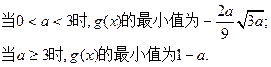
(II)证明:曲线
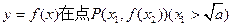 处的切线方程为
处的切线方程为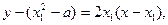
令
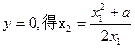 , ………………10分
, ………………10分所以
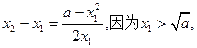
所以
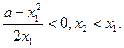 ………………11分
………………11分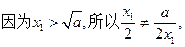
所以
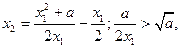 ………………13分
………………13分所以
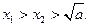 ………………14分
………………14分
练习册系列答案
相关题目
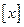 表示不超x的最大整数,(如
表示不超x的最大整数,(如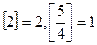 )。对于给定的
)。对于给定的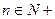 ,
,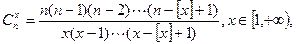 则
则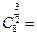 ________;
________;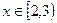 时,函数
时,函数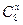 的值域是_________________________。
的值域是_________________________。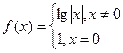 ,关于x的方程
,关于x的方程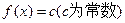 恰有三个不同的实数根
恰有三个不同的实数根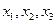 ,则
,则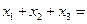
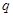 的等比数列
的等比数列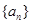 的前n项和为
的前n项和为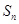 ,若
,若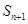 、
、 成等差数列,则
成等差数列,则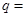 .
.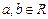 ,且
,且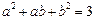 ,设
,设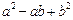 的最大值和最小值分别为
的最大值和最小值分别为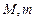 ,则
,则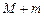 =
= 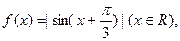 则
则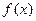 ( )
( )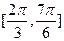 上是增函数
上是增函数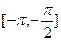 上是减函数
上是减函数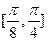 上是增函数
上是增函数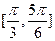 上是减函数
上是减函数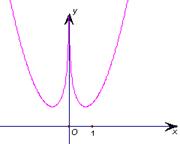
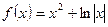
 的定义域为R,且当
的定义域为R,且当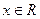 时,
时,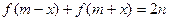 恒成立,
恒成立,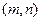 对称;
对称;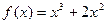 图象的一个对称点。
图象的一个对称点。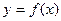 满足:①对任意的
满足:①对任意的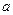 、
、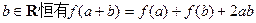 ;
;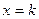 ;③
;③