题目内容
设f(x)=logag(x)(a>0且a≠1)。
(1)若f(x)在定义域D内是奇函数,求证:g(x)·g(-x)=1;
(2)若g(x)=ax且在[1,3]上,f(x)的最大值是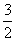 ,求实数a的值;
,求实数a的值;
(3)若g(x)=ax2-x,是否存在实数a,使得f(x)在区间I=[2,4]上是减函数?且对任意的x1,x2∈I都有f(x1)>ax2-2,如果存在,说明a可以取哪些值;如果不存在,请说明理由。
(1)若f(x)在定义域D内是奇函数,求证:g(x)·g(-x)=1;
(2)若g(x)=ax且在[1,3]上,f(x)的最大值是
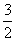 ,求实数a的值;
,求实数a的值;(3)若g(x)=ax2-x,是否存在实数a,使得f(x)在区间I=[2,4]上是减函数?且对任意的x1,x2∈I都有f(x1)>ax2-2,如果存在,说明a可以取哪些值;如果不存在,请说明理由。
解:(1)∵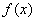 在定义域D内是奇函数,
在定义域D内是奇函数,
∴f(x)+f(-x)=0,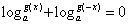 ,即
,即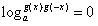 ,
,
∴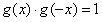 。
。
(2)①若a>1,则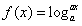 在[1,3]上是增函数,则有f(3)=
在[1,3]上是增函数,则有f(3)=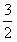 ,
,
∴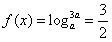 ,
,
∴a=9;
②若0<a<1,则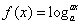 在[1,3]上是减函数,则有f(1)=
在[1,3]上是减函数,则有f(1)= 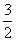 ,
,
∴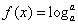 =
=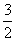 ,解得:a不存在;
,解得:a不存在;
综上所述:a=9。
(3)①若a>1时,要满足题设,则有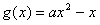 在[2,4]上是减函数,
在[2,4]上是减函数,
∴而函数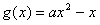 >0仅在
>0仅在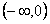 上是减函数,故a>1不符合题意;
上是减函数,故a>1不符合题意;
②若0<a<1时,要满足题设,则有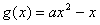 在[2,4]上是增函数,并且
在[2,4]上是增函数,并且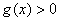 在[2,4]上成立,∴
在[2,4]上成立,∴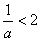 ,∴a>
,∴a>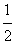 ,
,
要对任意的x1,x2∈I都有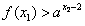 ,只要求f(x)的最小值大于
,只要求f(x)的最小值大于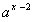 的最大值即可。
的最大值即可。
∵f(x)在区间I=[2,4]上是减函数,
∴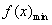 =
=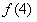 =
=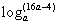 ,
,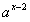 的最大值为
的最大值为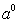 =1,
=1,
∴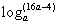 >1,∴a<
>1,∴a<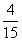 ,这与a>
,这与a>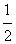 矛盾,舍去;
矛盾,舍去;
综上所述:满足题设的实数a不存在。
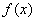 在定义域D内是奇函数,
在定义域D内是奇函数,∴f(x)+f(-x)=0,
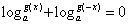 ,即
,即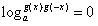 ,
,∴
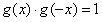 。
。(2)①若a>1,则
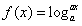 在[1,3]上是增函数,则有f(3)=
在[1,3]上是增函数,则有f(3)=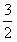 ,
,∴
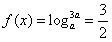 ,
,∴a=9;
②若0<a<1,则
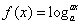 在[1,3]上是减函数,则有f(1)=
在[1,3]上是减函数,则有f(1)= 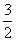 ,
,∴
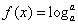 =
=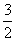 ,解得:a不存在;
,解得:a不存在; 综上所述:a=9。
(3)①若a>1时,要满足题设,则有
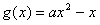 在[2,4]上是减函数,
在[2,4]上是减函数,∴而函数
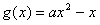 >0仅在
>0仅在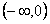 上是减函数,故a>1不符合题意;
上是减函数,故a>1不符合题意;②若0<a<1时,要满足题设,则有
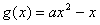 在[2,4]上是增函数,并且
在[2,4]上是增函数,并且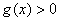 在[2,4]上成立,∴
在[2,4]上成立,∴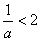 ,∴a>
,∴a>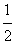 ,
,要对任意的x1,x2∈I都有
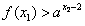 ,只要求f(x)的最小值大于
,只要求f(x)的最小值大于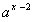 的最大值即可。
的最大值即可。∵f(x)在区间I=[2,4]上是减函数,
∴
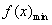 =
=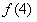 =
=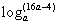 ,
,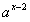 的最大值为
的最大值为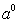 =1,
=1,∴
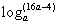 >1,∴a<
>1,∴a<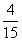 ,这与a>
,这与a>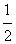 矛盾,舍去;
矛盾,舍去;综上所述:满足题设的实数a不存在。

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
设函数f(x)的定义域为D,若存在闭区间[a,b]?D,使得函数f(x)满足:①f(x)在[a,b]上是单调函数;②f(x)在[a,b]上的值域是[2a,2b],则称区间[a,b]是函数f(x)的“和谐区间”.下列结论错误的是( )
| A、函数f(x)=x2(x≥0)存在“和谐区间” | ||
| B、函数f(x)=ex(x∈R)不存在“和谐区间” | ||
C、函数f(x)=
| ||
D、函数f(x)=loga(ax-
|