题目内容

已知函数f（x）=
log5|x-5|，(x≠5)
3 ，(x=5)
，若关于x的方程f2（x）+bf（x）+c=0有五个不等实根x1，x2，…，x5，则f（x1+x2+…+x5）=
1+2lo
g
2
5
1+2lo
g
2
5
．
分析：由函数的解析式可得，函数f（x）的图象关于直线x=5对称，再由题意可得，五个不等实根x1，x2，…，x5，也关于直线x=5对称，故有x1+x2+…+x5=25，
再根据 f（x1+x2+…+x5）=f（25），运算求得结果．
解答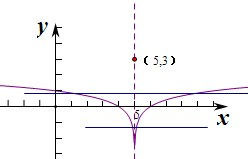：解：∵已知函数f（x）=
log5|x-5|，(x≠5)
3 ，(x=5)
，故有f（5）=3．
根据当x＞5时，f（x）=log5（x-5），当x＜5时，f（x）=log5（5-x），
可得函数f（x）的图象关于直线x=5对称．
再根据关于x的方程f2（x）+bf（x）+c=0有五个不等实根x1，x2，…，x5，
可得这5个根x1，x2，…，x5 也关于直线x=5对称，
∴x1+x2+…+x5 =25，
∴f（x1+x2+…+x5）=f（25）=log520=1+log54，=1+2log52，
故答案为  1+2log52．
点评：本题主要考查函数的零点与方程的根的关系，关键是根据函数的图象关于x=5对称，得出5个根也关于直线x=5对称，从而求得x1+x2+…+x5 =25，属于中档题．
练习册系列答案
相关题目
已知函数f（x）=2x-2+ae-x（a∈R）
（1）若曲线y=f（x）在点（1，f（1））处的切线平行于x轴，求a的值；
（2）当a=1时，若直线l：y=kx-2与曲线y=f（x）在（-∞，0）上有公共点，求k的取值范围．
已知函数f（x）=x2+2|lnx-1|．
（1）求函数y=f（x）的最小值；
（2）证明：对任意x∈[1，+∞），lnx≥
2(x-1)
x+1
恒成立；
（3）对于函数f（x）图象上的不同两点A（x1，y1），B（x2，y2）（x1＜x2），如果在函数f（x）图象上存在点M（x0，y0）（其中x0∈（x1，x2））使得点M处的切线l∥AB，则称直线AB存在“伴侣切线”．特别地，当x0=
x1+x2
2
时，又称直线AB存在“中值伴侣切线”．试问：当x≥e时，对于函数f（x）图象上不同两点A、B，直线AB是否存在“中值伴侣切线”？证明你的结论．
已知函数f（x）=x2-bx的图象在点A（1，f（1））处的切线l与直线x+3y-1=0垂直，若数列{
1
f(n)
}的前n项和为Sn，则S2012的值为（　　）
已知函数f（x）=xlnx
（Ⅰ）求函数f（x）的极值点；
（Ⅱ）若直线l过点（0，-1），并且与曲线y=f（x）相切，求直线l的方程．
已知函数f（x）=
3
x
a
+
3
(a-1)
x
，a≠0且a≠1．
（1）试就实数a的不同取值，写出该函数的单调增区间；
（2）已知当x＞0时，函数在（0，
6
）上单调递减，在（
6
，+∞）上单调递增，求a的值并写出函数的解析式；
（3）记（2）中的函数图象为曲线C，试问是否存在经过原点的直线l，使得l为曲线C的对称轴？若存在，求出直线l的方程；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网