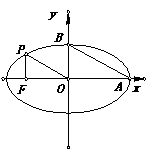
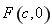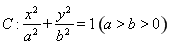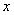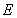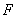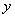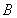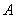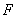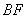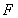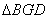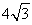题目内容
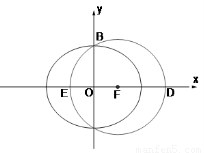
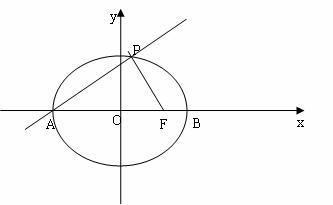
已知 是椭圆
是椭圆 的左焦点,
的左焦点,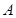 是椭圆短轴上的一个顶点,椭圆的离心率为
是椭圆短轴上的一个顶点,椭圆的离心率为 ,点
,点 在
在 轴上,
轴上, ,
,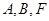 三点确定的圆
三点确定的圆 恰好与直线
恰好与直线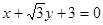 相切.
相切.
(Ⅰ)求椭圆的方程;
(Ⅱ)是否存在过 作斜率为
作斜率为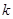
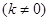 的直线
的直线 交椭圆于
交椭圆于 两点,
两点, 为线段
为线段 的中点,设
的中点,设 为椭圆中心,射线
为椭圆中心,射线 交椭圆于点
交椭圆于点 ,若
,若 ,若存在求
,若存在求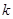 的值,若不存在则说明理由.
的值,若不存在则说明理由.
【答案】
20、解:
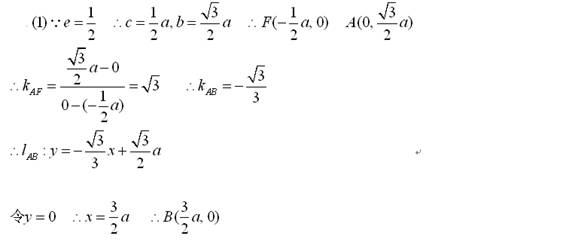
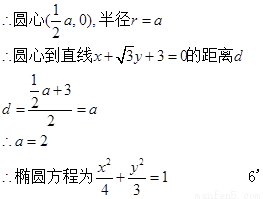
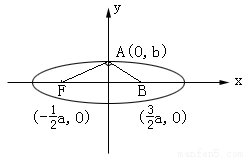
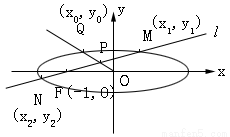
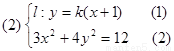
将(1)代入(2)可得:
(3+4k2)x2+8k2x+(4k2-12)=0 2’
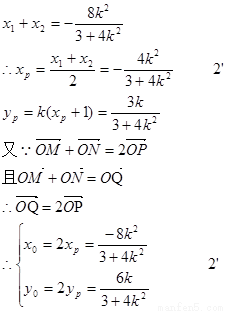
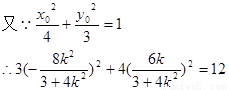
3×64k4+4×36k2=12(4k2+3)2
64k4+48k2=4(16k4+24k2+9)
48k2=96k2+36 2’
-48k2=36
∴k无解
∴不存在
【解析】略

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
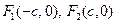 是椭圆
是椭圆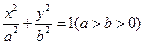 的左、右焦点,过点
的左、右焦点,过点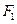 作
作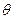 的动直线
的动直线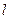 交椭圆于
交椭圆于 两点.当
两点.当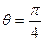 时,
时,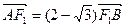 ,且
,且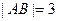 .
.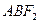 面积的最大值,并求出使面积达到最大值时直线
面积的最大值,并求出使面积达到最大值时直线