题目内容
已知 是椭圆
是椭圆 上一点,且点
上一点,且点 到椭圆的两个焦点距离之和为
到椭圆的两个焦点距离之和为 ;
;

(1)求椭圆方程;
(2)设 为椭圆的左顶点,直线
为椭圆的左顶点,直线 交
交 轴于点
轴于点 ,过
,过 作斜率为
作斜率为 的直线
的直线 交椭圆于
交椭圆于
 两点,若
两点,若 ,求实数
,求实数 的值.
的值.
【答案】
(1) 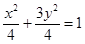 (2)
(2) 
【解析】
试题分析:(1)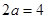 ,
,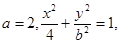 令
令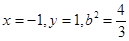 ,
,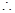 椭圆:
椭圆: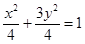
(2)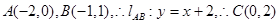 ,
, ,
,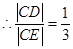 ,
,
设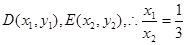 ,
,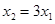 ,
,
若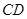 斜率不存在,
斜率不存在,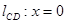 ,
,
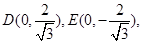
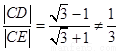 ,
,
若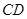 斜率存在,设
斜率存在,设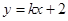 ,联立
,联立 ,得到
,得到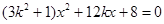
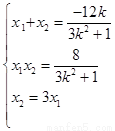 ,
,
考点:直线与椭圆的位置关系的运用
点评:解决的关键是理解椭圆的简单几何性质,以及根据简单几何性质来求解方程,同时联立方程组,结合韦达定理来得到根与系数的关系,解得,属于中档题。

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
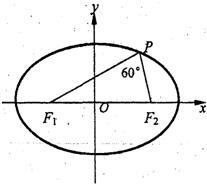 已知椭圆
已知椭圆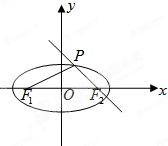 已知椭圆
已知椭圆 是椭圆
是椭圆 上一点,
上一点, ,
, 是椭圆的两焦点,且满足
是椭圆的两焦点,且满足
 、
、 是椭圆上任两点,且直线
是椭圆上任两点,且直线 、
、 的斜率分别为
的斜率分别为 、
、 ,若存在常数
,若存在常数 使
使 ,求直线
,求直线 的斜率.
的斜率.