题目内容
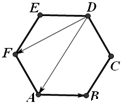如图，已知正六边形ABCDEF的边长为2，则| AB |
| DF |
| DA |
-2
-2
．分析：根据向量的减法法则，所求数量积等于向量
与
的数量积，结合题意知
与
的长度都为2，且∠BAF=120°，由此结合数量积计算公式，即可得到本题答案．
| AB |
| AF |
| AB |
| AF |
解答：解：∵
-
=
，
∴
•(
-
)=
•
=|
|•|
|•cos∠BAF
∵六边形ABCDEF是正六边形，边长为2，
∴∠BAF=120°，可得|
|•|
|•cos∠BAF=2×2×（-
）=-2
由此可得
•(
-
)=
•
=-2
故答案为：-2
| DF |
| DA |
| AF |
∴
| AB |
| DF |
| DA |
| AB |
| AF |
| AB |
| AF |
∵六边形ABCDEF是正六边形，边长为2，
∴∠BAF=120°，可得|
| AB |
| AF |
| 1 |
| 2 |
由此可得
| AB |
| DF |
| DA |
| AB |
| AF |
故答案为：-2
点评：本题给出正六边形，求向量的数量积，着重考查了正六边形的性质和平面向量数量积计算公式等知识点，属于基础题．
练习册系列答案
相关题目
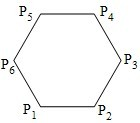如图，已知正六边形P1P2P3P4P5P6，下列向量的数量积中最大的是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
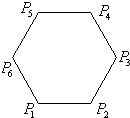如图，已知正六边形P1P2P3P4P5P6，设a=
，下列向量的数量积中最大的是
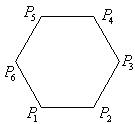
（B）
（D）
，下列向量的数量积中最大的是
（B）
（D）
B．
D．
