题目内容
甲、乙两名篮球运动员,甲投篮命中的概率为0.7,乙投篮命中的概率为0.8,两人是否投中相互之间没有影响.(Ⅰ)两人各投一次,求只有一人命中的概率;
(Ⅱ)两人各投两次,甲投中一次且乙投中两次的概率.
分析:本题考查的知识点是相互独立事件的概率乘法公式和加法公式,
(Ⅰ)两人各投一次,只有一人命中,分为两种情况,一是甲中乙不中,二是甲不中乙中,故两人各投一次,求只有一人命中的概率P=P(A
)+P(
B),代入计算即可得到答案.
(Ⅱ)两人各投两次,甲投中一次且乙投中两次的也分为两种情况,一是甲第一次投中,第二次投不中,二是甲第一次投不中,第二次投中,故两人各投两次,甲投中一次且乙投中两次的概率P=
P(A)P(
)[P(B)]2代入即可得到结论.
(Ⅰ)两人各投一次,只有一人命中,分为两种情况,一是甲中乙不中,二是甲不中乙中,故两人各投一次,求只有一人命中的概率P=P(A
. |
| B |
. |
| A |
(Ⅱ)两人各投两次,甲投中一次且乙投中两次的也分为两种情况,一是甲第一次投中,第二次投不中,二是甲第一次投不中,第二次投中,故两人各投两次,甲投中一次且乙投中两次的概率P=
| C | 1 2 |
. |
| A |
解答:解:将甲投中记为事件A,乙投中记为事件B,
(Ⅰ)P=P(A
)+P(
B)
=0.7×0.2+0.3×0.8=0.38
答:两人各投一次,只有一个命中的概率为0.38.
(Ⅱ)P=
P(A)P(
)[P(B)]2
=2×0.7×0.3×0.82
=0.2688
答:两人各投两次,甲投中一次且乙投中两次的概率为0.2688.
(Ⅰ)P=P(A
. |
| B |
. |
| A |
=0.7×0.2+0.3×0.8=0.38
答:两人各投一次,只有一个命中的概率为0.38.
(Ⅱ)P=
| C | 1 2 |
. |
| A |
=2×0.7×0.3×0.82
=0.2688
答:两人各投两次,甲投中一次且乙投中两次的概率为0.2688.
点评:本小题主要考查相互独立事件概率的计算,运用数学知识解决问题的能力,要想计算一个事件的概率,首先我们要分析这个事件是分类的(分几类)还是分步的(分几步),然后再利用加法原理和乘法原理进行求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 甲、乙两名篮球运动员在四场比赛中的得分数据以茎叶图记录如下:
甲、乙两名篮球运动员在四场比赛中的得分数据以茎叶图记录如下: 2012年的NBA全明星赛,于美国当地时间2012年2月26日在佛罗里达州奧兰多市举行.如图是参加此次比赛的甲、乙两名篮球运动员以往几场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是
2012年的NBA全明星赛,于美国当地时间2012年2月26日在佛罗里达州奧兰多市举行.如图是参加此次比赛的甲、乙两名篮球运动员以往几场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是 某赛季,甲、乙两名篮球运动员都参加了7场比赛,他们所有比赛得分的情况用如图所示的茎叶图表示,则甲、乙两名运动员得分的平均数分别为( )
某赛季,甲、乙两名篮球运动员都参加了7场比赛,他们所有比赛得分的情况用如图所示的茎叶图表示,则甲、乙两名运动员得分的平均数分别为( )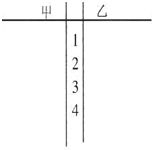 某赛季,甲、乙两名篮球运动员都参加了10场比赛,比赛得分情况记录如下(单位:分):
某赛季,甲、乙两名篮球运动员都参加了10场比赛,比赛得分情况记录如下(单位:分):
 (2012•厦门模拟)某赛季甲、乙两名篮球运动员各6场比赛得分情况用茎叶图记录,下列四个结论中,不正确的是( )
(2012•厦门模拟)某赛季甲、乙两名篮球运动员各6场比赛得分情况用茎叶图记录,下列四个结论中,不正确的是( )