题目内容
 甲、乙两名篮球运动员在四场比赛中的得分数据以茎叶图记录如下:
甲、乙两名篮球运动员在四场比赛中的得分数据以茎叶图记录如下:(Ⅰ)求乙球员得分的平均数和方差;
(Ⅱ)分别从两人得分中随机选取一场的得分,求得分和Y的分布列和数学期望.
(注:方差s2=
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
分析:(I)由茎叶图可知,乙球员四场比赛得分,从而,可求乙球员得分的平均数和方差;
(Ⅱ)确定从两人得分中随机选取一场的得分情况、得分和可能的结果,即可求得得分和Y的分布列和数学期望.
(Ⅱ)确定从两人得分中随机选取一场的得分情况、得分和可能的结果,即可求得得分和Y的分布列和数学期望.
解答:解:(Ⅰ)由茎叶图可知,乙球员四场比赛得分为18,24,24,30,
所以平均数
=
=24; …(2分)
∴s2=
[(18-24)2+(24-24)2+(24-24)2+(30-24)2]=18 …(5分)
(Ⅱ)甲球员四场比赛得分为20,20,26,32,分别从两人得分中随机选取一场的得分,共有16种情况:
(18,20)(18,20)(18,26)(18,32)
(24,20)(24,20)(24,26)(24,32)
(24,20)(24,20)(24,26)(24,32)
(30,20)(30,20)(30,26)(30,32)…(8分)
得分和可能的结果有:38,44,50,56,62 …(9分)
得分和Y的分布列为:
…(11分)
数学期望EY=38×
+44×
+50×
+56×
+62×
=48.5.…(13分)
所以平均数
. |
| x |
| 18+24+24+30 |
| 4 |
∴s2=
| 1 |
| 4 |
(Ⅱ)甲球员四场比赛得分为20,20,26,32,分别从两人得分中随机选取一场的得分,共有16种情况:
(18,20)(18,20)(18,26)(18,32)
(24,20)(24,20)(24,26)(24,32)
(24,20)(24,20)(24,26)(24,32)
(30,20)(30,20)(30,26)(30,32)…(8分)
得分和可能的结果有:38,44,50,56,62 …(9分)
得分和Y的分布列为:
| Y | 38 | 44 | 50 | 56 | 62 | ||||||||||
| P |
|
|
|
|
|
数学期望EY=38×
| 1 |
| 8 |
| 5 |
| 16 |
| 5 |
| 16 |
| 3 |
| 16 |
| 1 |
| 16 |
点评:本题考查茎叶图,考查方差与期望,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 2012年的NBA全明星赛,于美国当地时间2012年2月26日在佛罗里达州奧兰多市举行.如图是参加此次比赛的甲、乙两名篮球运动员以往几场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是
2012年的NBA全明星赛,于美国当地时间2012年2月26日在佛罗里达州奧兰多市举行.如图是参加此次比赛的甲、乙两名篮球运动员以往几场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是 某赛季,甲、乙两名篮球运动员都参加了7场比赛,他们所有比赛得分的情况用如图所示的茎叶图表示,则甲、乙两名运动员得分的平均数分别为( )
某赛季,甲、乙两名篮球运动员都参加了7场比赛,他们所有比赛得分的情况用如图所示的茎叶图表示,则甲、乙两名运动员得分的平均数分别为( )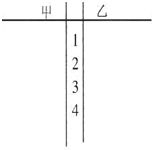 某赛季,甲、乙两名篮球运动员都参加了10场比赛,比赛得分情况记录如下(单位:分):
某赛季,甲、乙两名篮球运动员都参加了10场比赛,比赛得分情况记录如下(单位:分):
 (2012•厦门模拟)某赛季甲、乙两名篮球运动员各6场比赛得分情况用茎叶图记录,下列四个结论中,不正确的是( )
(2012•厦门模拟)某赛季甲、乙两名篮球运动员各6场比赛得分情况用茎叶图记录,下列四个结论中,不正确的是( )