题目内容
设f(x)是定义在R上的奇函数,当x≤0时,f(x)=2x2-x,则f(1)=
| A.-3 | B.-1 | C.1 | D.3 |
A
试题分析:要计算f(1)的值,根据f(x)是定义在R上的奇函娄和,我们可以先计算f(-1)的值,再利用奇函数的性质进行求解,当x≤0时,f(x)=2x2-x,代入即可得到答案.∵当x
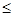 0时,f(x)=2x2-x,
0时,f(x)=2x2-x,∴f(-1)=2(-1)2-(-1)=3,
又∵f(x)是定义在R上的奇函数
∴f(1)=-f(-1)=-3
故选A
点评:本题考查的知识点是函数奇偶性的性质,熟练掌握函数的奇偶性的性质是解答本题的关键.

练习册系列答案
相关题目
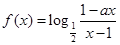 为奇函数,
为奇函数,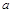 为常数.
为常数.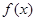 在区间
在区间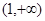 内单调递增;
内单调递增;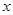 的值,不等式
的值,不等式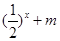 恒成立,求实数
恒成立,求实数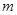 的取值范围.
的取值范围.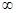 )上单调递增的函数是( )
)上单调递增的函数是( )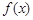 在(0,+∞)上是增函数,又
在(0,+∞)上是增函数,又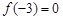 ,则不等式
,则不等式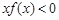 的解集为( )
的解集为( )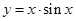 是 函数(填“奇”、“偶”或“非奇非偶”).
是 函数(填“奇”、“偶”或“非奇非偶”).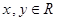 ,且满足
,且满足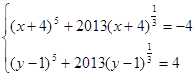 ,则
,则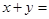 .
.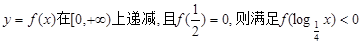 的x的集合为
的x的集合为

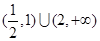

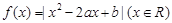 .给下列命题:
.给下列命题: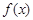 必是偶函数;
必是偶函数;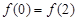 时,
时,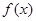 的图像必关于直线x=1对称;
的图像必关于直线x=1对称;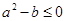 ,则
,则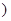 上是增函数;④
上是增函数;④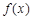 有最大值
有最大值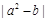 .
.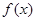 是定义在R上的奇函数,当
是定义在R上的奇函数,当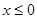 时,
时,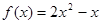 ,则
,则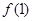 的值是 ( )
的值是 ( )