题目内容
 如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,DE=2AB=2,且F是CD的中点.
如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,DE=2AB=2,且F是CD的中点.(Ⅰ)求证:AF∥平面BCE;
(Ⅱ)求证:平面BCE⊥平面CDE;
(Ⅲ)设AC=2m,当m为何值时?使得平面BCE与平面ACD所成的二面角的大小为45°.
分析:(I)取CE中点P,连接FP、BP,易知FP∥DE,且FP=
DE.AB∥DE,且AB=
DE.可知ABPF为平行四边形,得到AF∥BP,由线面平行的判定定理得AF∥平面BCE.
(II)先证AF⊥平面CDE.又BP∥AF,得到BP⊥平面CDE,再由面面垂直的判定定理得到平面BCE⊥平面CDE;
(Ⅲ)△ACD是△CBE在平面中的射影,由于S△CBE=m
,平面BCE与平面ACD所成的二面角的大小为45°
故可求得m的值.
| 1 |
| 2 |
| 1 |
| 2 |
(II)先证AF⊥平面CDE.又BP∥AF,得到BP⊥平面CDE,再由面面垂直的判定定理得到平面BCE⊥平面CDE;
(Ⅲ)△ACD是△CBE在平面中的射影,由于S△CBE=m
| 3(1+m2) |
故可求得m的值.
解答: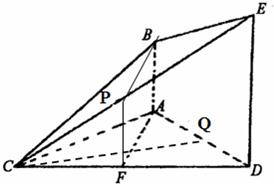 解:(I)取CE中点P,连接FP、BP,
解:(I)取CE中点P,连接FP、BP,
∵F为CD的中点,
∴FP∥DE,且FP=
DE.(2分)
又AB∥DE,且AB=
DE.
∴AB∥FP,且AB=FP,
∴ABPF为平行四边形,
∴AF∥BP.
又∵AF?平面BCE,BP?平面BCE,
∴AF∥平面BCE.
(II)∵△ACD为正三角形,
∴AF⊥CD.
∵AB⊥平面ACD,DE∥AB,
∴DE⊥平面ACD,又AF?平面ACD,
∴DE⊥AF又AF⊥CD,CD∩DE=D,
∴AF⊥平面CDE.
又BP∥AF,∴BP⊥平面CDE.
又∵BP?平面BCE,
∴平面BCE⊥平面CDE.
(Ⅲ) 由题意可知,△CBE中,CB=EB=
,CE=
,
∴S△CBE=m
∵平面BCE与平面ACD所成的二面角的大小为45°
∴cos45°=
=
∴m=1
 解:(I)取CE中点P,连接FP、BP,
解:(I)取CE中点P,连接FP、BP,∵F为CD的中点,
∴FP∥DE,且FP=
| 1 |
| 2 |
又AB∥DE,且AB=
| 1 |
| 2 |
∴AB∥FP,且AB=FP,
∴ABPF为平行四边形,
∴AF∥BP.
又∵AF?平面BCE,BP?平面BCE,
∴AF∥平面BCE.
(II)∵△ACD为正三角形,
∴AF⊥CD.
∵AB⊥平面ACD,DE∥AB,
∴DE⊥平面ACD,又AF?平面ACD,
∴DE⊥AF又AF⊥CD,CD∩DE=D,
∴AF⊥平面CDE.
又BP∥AF,∴BP⊥平面CDE.
又∵BP?平面BCE,
∴平面BCE⊥平面CDE.
(Ⅲ) 由题意可知,△CBE中,CB=EB=
| 1+4m2 |
| 1+m2 |
∴S△CBE=m
| 3(1+m2) |
∵平面BCE与平面ACD所成的二面角的大小为45°
∴cos45°=
| ||
m
|
| ||
| 2 |
∴m=1
点评:本题以线面垂直为载体,主要考查平面图形中的线线关系,考查线面平行、面面垂直的判定,考查面面角,考查运算能力和推理论证能力.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
 (2012•惠州模拟)如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.
(2012•惠州模拟)如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点. (2012•枣庄一模)如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.
(2012•枣庄一模)如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点. 如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD为等边三角形,AD=DE=2AB,F为CD的中点
如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD为等边三角形,AD=DE=2AB,F为CD的中点 如图,已知AB⊥平面ACD,DE⊥平面ACD,且AC=AD=DE=2AB=4,F为CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,且AC=AD=DE=2AB=4,F为CD的中点.