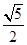题目内容
如图,F1,F2是双曲线C: (a>0,b>0)的左、右焦点,过F1的直线
(a>0,b>0)的左、右焦点,过F1的直线 与
与 的左、右两支分别交于A,B两点.若
的左、右两支分别交于A,B两点.若 ABF2为等边三角形,则双曲线的离心率为( )
ABF2为等边三角形,则双曲线的离心率为( )
A. | B.2 | C. | D. |
C
解析试题分析:设 ,由于
,由于 为等边三角形,
为等边三角形, ,由双曲线的定义得
,由双曲线的定义得
 ,而
,而 ,
, ,
, ,在
,在 中,
中, ,
, ,
, ,
, ,
,
由余弦定理得 ,整理得
,整理得 ,
,
即 ,
, ,
, ,即该双曲线的离心率为
,即该双曲线的离心率为 .
.
考点:双曲线的定义与离心率、余弦定理

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
双曲线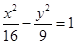 的离心率为( )
的离心率为( )
A. | B. | C. | D. |
若 是2和8的等比中项,则圆锥曲线
是2和8的等比中项,则圆锥曲线 的离心率是( )
的离心率是( )
A. | B. | C. 或 或 | D. |
已知抛物线的顶点在原点,焦点在y轴上,抛物线上的点 到焦点的距离为4,则
到焦点的距离为4,则 的值为( )
的值为( )
| A.4 | B.-2 | C.4或-4 | D.12或-2 |
抛物线y2= 2x的准线方程是( )
A.y= | B.y=- | C.x= | D.x=-  |
若双曲线 的一个焦点在直线
的一个焦点在直线 上,则其渐近线方程为( )
上,则其渐近线方程为( )
A. | B. | C. | D. |
已知 为平面内两定点,过该平面内动点
为平面内两定点,过该平面内动点 作直线
作直线 的垂线,垂足为
的垂线,垂足为 .若
.若 ,其中
,其中 为常数,则动点
为常数,则动点 的轨迹不可能是( )
的轨迹不可能是( )
| A.圆 | B.椭圆 | C.抛物线 | D.双曲线 |
 是抛物线
是抛物线 的焦点,
的焦点, 、
、 是该抛物线上的两点,且
是该抛物线上的两点,且 ,则线段
,则线段 的中点到
的中点到 轴的距离为( )
轴的距离为( )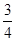



 是双曲线
是双曲线 上的不同三点,且
上的不同三点,且 连线经过坐标原点,若直线
连线经过坐标原点,若直线 的斜率乘积
的斜率乘积 ,则该双曲线的离心率
,则该双曲线的离心率 =( )
=( )