题目内容
(本小题满分16分)
已知函数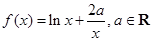 .
.
(1)若x=2是函数f(x)的极值点,求实数a的值.
(2)若函数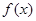 在
在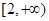 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;
(3)若函数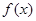 在
在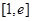 上的最小值为3,求实数
上的最小值为3,求实数 的值.
的值.
(1)1(2) (3)
(3)
解析试题分析:(1) ,由同意得
,由同意得 a=2,∴a=1,经检验,
a=2,∴a=1,经检验, 是
是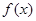 的极值点
的极值点
(2)∵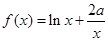 ,∴
,∴ .
.
∵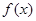 在
在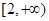 上是增函数,
上是增函数,
∴ ≥0在
≥0在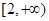 上恒成立,即
上恒成立,即 ≤
≤ 在
在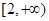 上恒成立. ,
上恒成立. ,
令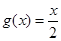 ,则
,则 ≤
≤ .
.
∵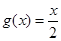 在
在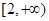 上是增函数,∴
上是增函数,∴ .
.
∴ .所以实数
.所以实数 的取值范围为
的取值范围为 .
.
(3)由(1)得 ,
, .
.
①若 ,则
,则 ,即
,即 在
在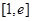 上恒成立,此时
上恒成立,此时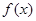 在
在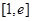 上是增函数.
上是增函数.
所以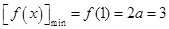 ,解得
,解得 (舍去).
(舍去).
②若 ,令
,令 ,得
,得 .当
.当 时,
时, ,所以
,所以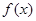 在
在 上是减函数,当
上是减函数,当 时,
时, ,所以
,所以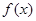 在
在 上是增函数.
上是增函数.
所以 ,解得
,解得 (舍去).
(舍去).
③若 ,则
,则 ,即
,即 在
在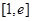 上恒成立,此时
上恒成立,此时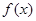 在
在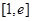 上是减函数.
上是减函数.
所以 ,所以
,所以 .
.
综上所述, .
.
考点:利用导数求函数极值最值
点评:不等式恒成立问题常转换为求函数最值问题

练习册系列答案
相关题目

 在区间
在区间 上的最小值和最大值;
上的最小值和最大值; 上是增函数,求实数a的取值范围。
上是增函数,求实数a的取值范围。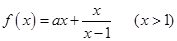
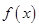 的最小值;
的最小值;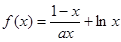
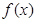 在
在 上为增函数,求正实数
上为增函数,求正实数 的取值范围;
的取值范围;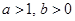 ,求证:
,求证: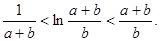
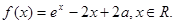
 的单调区间与极值;
的单调区间与极值;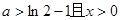 时,
时,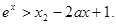
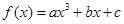
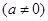 为奇函数,其图象在点
为奇函数,其图象在点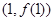 处的切线与直线
处的切线与直线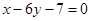 垂直,导函数
垂直,导函数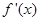 的最小值为
的最小值为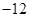 .试求
.试求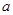 ,
, ,
,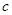 的值。
的值。 (2)
(2)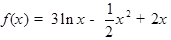
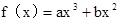 ,曲线
,曲线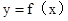 过点P(-1,2),且在点P处的切线恰好与直线x-3y=0垂直。
过点P(-1,2),且在点P处的切线恰好与直线x-3y=0垂直。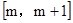 上是增函数,求m的取值范围.
上是增函数,求m的取值范围.
 且函数
且函数 在其定义域上为增函数时,求
在其定义域上为增函数时,求 的取值范围;
的取值范围; 处取得极值,试用
处取得极值,试用 ;
;