题目内容

观察下列等式：

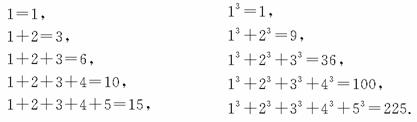
可以推测：13＋23＋33＋…＋n3＝________(n∈N*，用含有n的代数式表示)．

解析　第二列等式的右端分别是1×1,3×3,6×6,10×10,15×15，∵1,3,6,10,15，…第n项an与第n－1项an－1(n≥2)的差为：an－an－1＝n，∴a2－a1＝2，a3－a2＝3，a4－a3＝4，…，an－an－1＝n，各式相加得，

an＝a1＋2＋3＋…＋n，其中a1＝1，∴an＝1＋2＋3＋…＋n，即an＝，∴a＝n2(n＋1)2.

答案　n2(n＋1)2

练习册系列答案
相关题目
（2013•陕西）观察下列等式：
（1+1）=2×1
（2+1）（2+2）=22×1×3
（3+1）（3+2）（3+3）=23×1×3×5
…
照此规律，第n个等式可为
（n+1）（n+2）（n+3）…（n+n）=2n•1•3•5…•（2n-1）
（n+1）（n+2）（n+3）…（n+n）=2n•1•3•5…•（2n-1）
．
观察下列等式：
1
2×3
=（
1
2
-
1
3
）×
1
1
，
1
2×4
=（
1
2
-
1
4
）×
1
2
，
1
2×5
=（
1
2
-
1
5
）×
1
3
，
1
2×6
=（
1
2
-
1
6
）×
1
4
，…可推测当n≥3，n∈N*时，
1
2×n
=
（
1
2
-
1
n
）×
1
n-2
（
1
2
-
1
n
）×
1
n-2
．
（2013•陕西）观察下列等式：
12=1
12-22=-3
12-22+32=6
12-22+32-42=-10
…
照此规律，第n个等式可为
12-22+32-…+(-1)n-1n2=
(-1)n+1
2
n(n+1)
12-22+32-…+(-1)n-1n2=
(-1)n+1
2
n(n+1)
．
观察下列等式：
2=1×2
2+4=2×3
2+4+6=3×4
2+4+6+8=4×5
…
照此规律，第n个等式可为
 
．

观察下列等式:

(1+1)=2×1,

(2+1)(2+2)=22×1×3,

(3+1)(3+2)(3+3)=23×1×3×5,

……

照此规律,第n个等式可为　　　　.

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网