题目内容
(2013•陕西)观察下列等式:
12=1
12-22=-3
12-22+32=6
12-22+32-42=-10
…
照此规律,第n个等式可为
12=1
12-22=-3
12-22+32=6
12-22+32-42=-10
…
照此规律,第n个等式可为
12-22+32-…+(-1)n-1n2=
n(n+1)
| (-1)n+1 |
| 2 |
12-22+32-…+(-1)n-1n2=
n(n+1)
.| (-1)n+1 |
| 2 |
分析:等式的左边是正整数的平方和或差,根据这一规律得第n个等式左边为12-22+32-42+…(-1)n-1n2.再分n为奇数和偶数讨论,结合分组求和法求和,最后利用字母表示即可.
解答:解:观察下列等式:
12=1
12-22=-3
12-22+32=6
12-22+32-42=-10
…
分n为奇数和偶数讨论:
第n个等式左边为12-22+32-42+…(-1)n-1n2.
当n为偶数时,分组求和(12-22)+(32-42)+…+[n-1)2-n2]=-
,
当n为奇数时,第n个等式左边=12-22)+(32-42)+…+[n-1)2-n2]=-
+n2=
.
综上,第n个等式为12-22+32-…+(-1)n-1n2=
n(n+1).
故答案为:12-22+32-…+(-1)n-1n2=
n(n+1).
12=1
12-22=-3
12-22+32=6
12-22+32-42=-10
…
分n为奇数和偶数讨论:
第n个等式左边为12-22+32-42+…(-1)n-1n2.
当n为偶数时,分组求和(12-22)+(32-42)+…+[n-1)2-n2]=-
| n(n+1) |
| 2 |
当n为奇数时,第n个等式左边=12-22)+(32-42)+…+[n-1)2-n2]=-
| n(n+1) |
| 2 |
| n(n+1) |
| 2 |
综上,第n个等式为12-22+32-…+(-1)n-1n2=
| (-1)n+1 |
| 2 |
故答案为:12-22+32-…+(-1)n-1n2=
| (-1)n+1 |
| 2 |
点评:本题考查规律型中的数字变化问题,找等式的规律时,既要分别看左右两边的规律,还要注意看左右两边之间的联系.

练习册系列答案
相关题目
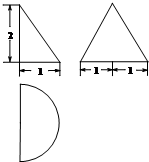 (2013•陕西)某几何体的三视图如图所示,则其体积为
(2013•陕西)某几何体的三视图如图所示,则其体积为