题目内容
4.在△ABC中,角A,B,C的对边分别为a,b,c,bcosC=a-$\frac{1}{2}$c.(Ⅰ)求角B的大小;
(Ⅱ)若b=1,求a+c的最大值.
分析 (Ⅰ)运用余弦定理化简整理,再由特殊角的三角函数值,即可得到所求角B;
(Ⅱ)运用余弦定理:b2=a2+c2-2accosB,结合基本不等式即可得到a+c的最大值.
解答 解:(Ⅰ)∵$bcosC=a-\frac{1}{2}c∴b\frac{{{a^2}+{b^2}-{c^2}}}{2ab}=a-\frac{1}{2}c$,
∴b2-c2=a2-ac
∴b2=a2+c2-ac,
∴$cosB=\frac{1}{2}$,
又∵$B∈(0,π)∴B=\frac{π}{3}$;
(Ⅱ)∵b2=a2+c2-2accosB,
∴1=a2+c2-ac=(a+c)2-3ac,
∵$ac≤\frac{{{{(a+c)}^2}}}{4}$当且仅当a=c时等号成立,
∴$\frac{1}{4}{(a+c)^2}≤1$,即a+c≤2.
即有a+c的最大值为2.
点评 本题考查余弦定理的运用,考查运用基本不等式求最值的方法,以及运算化简能力,属于中档题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
12.若函数f(x)=$\left\{\begin{array}{l}{1,(x∈Q)}\\{0,(x∈{∁}_{R}Q)}\end{array}\right.$,则f(e)=( )(其中e是自然对数的底数)
| A. | 0 | B. | 1 | C. | 0或1 | D. | 不确定 |
16.已知f(x)满足f(x+2)=f(x)和f(-x)=-f(x),且当x∈(0,1)时,f(x)=3x-1,则f($\frac{2015}{2}$)=( )
| A. | $\sqrt{3}+1$ | B. | $\sqrt{3}-1$ | C. | -$\sqrt{3}-1$ | D. | -$\sqrt{3}+$ |
14.奇函数f(x)满足①在(-∞,0)内单调递增,②f(2)=0,则不等式(x-1)f(x-1)>0的解集为( )
| A. | (-∞,-2)∪(0,2) | B. | (-3,-1)∪(1,3) | C. | (-2,2) | D. | (-∞,-1)∪(3,+∞) |
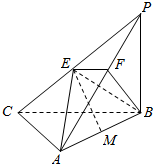 在三棱锥P-ABC中,PB⊥地面ABC,∠BCA=90°,E,M分别为PC,AB的中点,点F在PA上,且AF=2FP.
在三棱锥P-ABC中,PB⊥地面ABC,∠BCA=90°,E,M分别为PC,AB的中点,点F在PA上,且AF=2FP.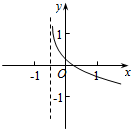 若函数f(x)=loga(x+b)的大致图象如图,其中a,b为常数,则函数g(x)=a-x+b的大致图象是( )
若函数f(x)=loga(x+b)的大致图象如图,其中a,b为常数,则函数g(x)=a-x+b的大致图象是( )