题目内容
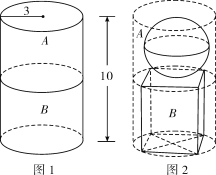
【题目】石雕工艺承载着几千年的中国石雕文化,随着科技的发展,机器雕刻产品越来越多.某石雕厂计划利用一个圆柱形的石材(如图1)雕刻制作一件工艺品(如图2),该作品的上方是一个球体,下方是一个正四棱柱,经测量,圆柱形石材的底面半径![]() 米,高
米,高![]() 米,制作要求如下:首先需将石材切割为体积相等的两部分(分别称为圆柱A和圆柱B),要求切面与原石材的上、下底面平行(不考虑损耗),然后将圆柱A切割打磨为一个球体,将圆柱B切割打磨为一个长方体,则加工打磨后所得工艺品的体积的最大值为________立方米.
米,制作要求如下:首先需将石材切割为体积相等的两部分(分别称为圆柱A和圆柱B),要求切面与原石材的上、下底面平行(不考虑损耗),然后将圆柱A切割打磨为一个球体,将圆柱B切割打磨为一个长方体,则加工打磨后所得工艺品的体积的最大值为________立方米.
【答案】![]()
【解析】
要求加工打磨后所得工艺品的体积的最大值,只需上方的球与下方的长方体的体积同时取得最大值即可.
因为圆柱A和圆柱B的体积一样大,所以它们的高![]() 一样,即
一样,即![]() 米,
米,
要使工艺品的体积最大,则上方的球与下方的长方体的体积同时取得最大值,
设由圆柱A打磨的球体半径为![]() ,则
,则![]() ,即
,即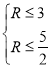 ,所以
,所以![]() ,
,
当![]() 时,球的体积取得最大值,此时球体体积
时,球的体积取得最大值,此时球体体积![]() ,
,
设下方的长方体的底面边长分别为![]() ,
,![]() ,
,
要使长方体的体积最大,长方体的高与圆柱B的高相等,此时其体积![]() ,
,
因为长方体为圆柱B的内接长方体,即长方体的底面是圆柱底面的内接长方形,
所以长方形的对角线长等于圆柱底面的直径,即![]() ,
,
由基本不等式可得![]() ,即
,即![]() ,当且仅当
,当且仅当![]() 时取等号,
时取等号,
所以长方体体积的最大值为![]() ,
,
所以所得工艺品的体积的最大值为![]() (立方米).
(立方米).

 名校课堂系列答案
名校课堂系列答案【题目】某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次,整理数据得到下表(单位:天):
锻炼人次 空气质量等级 | [0,200] | (200,400] | (400,600] |
1(优) | 2 | 16 | 25 |
2(良) | 5 | 10 | 12 |
3(轻度污染) | 6 | 7 | 8 |
4(中度污染) | 7 | 2 | 0 |
(1)分别估计该市一天的空气质量等级为1,2,3,4的概率;
(2)求一天中到该公园锻炼的平均人次的估计值(同一组中的数据用该组区间的中点值为代表);
(3)若某天的空气质量等级为1或2,则称这天“空气质量好”;若某天的空气质量等级为3或4,则称这天“空气质量不好”.根据所给数据,完成下面的2×2列联表,并根据列联表,判断是否有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关?
人次≤400 | 人次>400 | |
空气质量好 | ||
空气质量不好 |
附: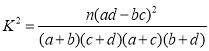 ,
,
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |