题目内容
已知f(x)=-4+
|
| 1 |
| an+1 |
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)数列{bn}的前n项和为Tn且满足
| Tn+1 |
| an2 |
| Tn |
| an+12 |
| 1 |
| 2 |
| 4n+1 |
分析:(Ⅰ)由-
=f(an) =-
,且an>0,知
=
,由此知 an2=
,从而得到数列{an}的通项公式;
(Ⅱ)把(I)中求出的数列的通项公式代入
=
+16n2-8n-3中,化简后得到
-
=1,设
=cn,则上式变为cn+1-cn=1,得到{cn}是等差数列.求出{cn}的通项公式,
代入即可求得Tn的通项公式,然后利用bn=Tn-Tn-1即可得到数列{bn}的通项公式.
(III)由 an=
,知 an=
>
=
,由此能够证明Sn>
-1,n∈N*.
| 1 |
| an+1 |
4+
|
| 1 |
| an+1 |
4+
|
| 1 |
| 4n-3 |
(Ⅱ)把(I)中求出的数列的通项公式代入
| Tn+1 |
| an2 |
| Tn |
| an+12 |
| Tn+1 |
| 4n+1 |
| Tn |
| 4n-3 |
| Tn |
| 4n-3 |
代入即可求得Tn的通项公式,然后利用bn=Tn-Tn-1即可得到数列{bn}的通项公式.
(III)由 an=
| 1 | ||
|
| 2 | ||
2
|
| 2 | ||||
|
| ||||
| 2 |
| 1 |
| 2 |
| 4n+1 |
解答:解:(Ⅰ)-
=f(an) =-
,且an>0,
∴
=
,
∴
-
=4(n∈N+),
∴数列{
}是等差数列,首项
公差d=4
∴
=1+4(n-1)
∴an2=
∵an>0
∴an=
(n∈N+)(4分)(6分)
(Ⅱ)由题设知(4n-3)Tn+1=(4n+1)Tn+(4n+1)(4n-3).
∴
-
=1.
设
=cn,则上式变为cn+1-cn=1.
∴{cn}是等差数列.
∴cn=c1+n-1=
+n-1=b1+n-1=n.
∴
=T 1+n -1,若{bn}为等差数列,则T1=1,即b=1,
即Tn=n(4n-3)=4n2-3n.
∴当n=1时,bn=T1=1;
当n≥2时,bn=Tn-Tn-1=4n2-3n-4(n-1)2+3(n-1)=8n-7.
经验证n=1时也适合上式.
∴bn=8n-7(n∈N*).
(III)证明:an=
∴an=
>
=
,
∴Sn=a1+a2+…+an>
(
-1)+(
-
)+…+
(
-
)
=
-1
| 1 |
| an+1 |
4+
|
∴
| 1 |
| an+1 |
4+
|
∴
| 1 |
| an+12 |
| 1 |
| an2 |
∴数列{
| 1 |
| an2 |
| 1 |
| a12 |
∴
| 1 |
| a12 |
∴an2=
| 1 |
| 4n-3 |
∵an>0
∴an=
| 1 | ||
|
(Ⅱ)由题设知(4n-3)Tn+1=(4n+1)Tn+(4n+1)(4n-3).
∴
| Tn+1 |
| 4n+1 |
| Tn |
| 4n-3 |
设
| Tn |
| 4n-3 |
∴{cn}是等差数列.
∴cn=c1+n-1=
| T1 |
| 1 |
∴
| Tn |
| 4n-3 |
即Tn=n(4n-3)=4n2-3n.
∴当n=1时,bn=T1=1;
当n≥2时,bn=Tn-Tn-1=4n2-3n-4(n-1)2+3(n-1)=8n-7.
经验证n=1时也适合上式.
∴bn=8n-7(n∈N*).
(III)证明:an=
| 1 | ||
|
∴an=
| 2 | ||
2
|
| 2 | ||||
|
| ||||
| 2 |
∴Sn=a1+a2+…+an>
| 1 |
| 2 |
| 5 |
| 9 |
| 5 |
| 1 |
| 2 |
| 4n+1 |
| 4n-3 |
=
| 1 |
| 2 |
| 4n+1 |
点评:本题考查数列通项公式的求法和不等式的证明,考查学生灵活运用等差数列的前n项和的公式化简求值,会确定一个数列为等差数列,是一道综合题.解题时要认真审题,注意数列性质的合理运用.

练习册系列答案
相关题目
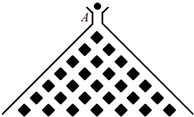 (2011•丹东模拟)如图,在竖直平面内有一个“游戏滑道”,空白部分表示光滑滑道,黑色正方形表示障碍物,自上而下第一行有1个障碍物,第二行有2个障碍物,…,依此类推.一个半径适当的光滑均匀小球从入口A投入滑道,小球将自由下落,已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是
(2011•丹东模拟)如图,在竖直平面内有一个“游戏滑道”,空白部分表示光滑滑道,黑色正方形表示障碍物,自上而下第一行有1个障碍物,第二行有2个障碍物,…,依此类推.一个半径适当的光滑均匀小球从入口A投入滑道,小球将自由下落,已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是