题目内容
设实数x，y满足条件
若目标函数z=ax+by（a＞0，b＞0）的最大值为12，则
+
的最小值为（ ）
|
| 2 |
| a |
| 3 |
| b |
分析：由已知可得2a+3b=6，则
+
=（2a+3b）（
+
）×
，然后利用基本不等式可求最小值
| 2 |
| a |
| 3 |
| b |
| 2 |
| a |
| 3 |
| b |
| 1 |
| 6 |
解答：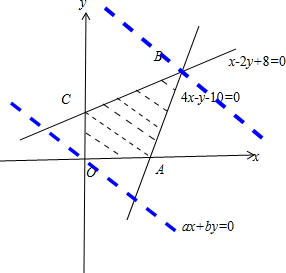
解：不等式表示的平面区域如图所示阴影部分，
当直线ax+by=z（a＞0，b＞0）
过直线4x-y-10=0与直线x-2y+8=0的交点（4，6）时，目标函数z=ax+by（a＞0，b＞0）取得最大12
∴4a+6b=12即2a+3b=6
则
+
=（2a+3b）（
+
）×
=
≥
=
当且仅当
=
即a=b=
时取等号
故选A
解：不等式表示的平面区域如图所示阴影部分，当直线ax+by=z（a＞0，b＞0）
过直线4x-y-10=0与直线x-2y+8=0的交点（4，6）时，目标函数z=ax+by（a＞0，b＞0）取得最大12
∴4a+6b=12即2a+3b=6
则
| 2 |
| a |
| 3 |
| b |
| 2 |
| a |
| 3 |
| b |
| 1 |
| 6 |
13+
| ||||
| 6 |
| 13+12 |
| 6 |
| 25 |
| 6 |
当且仅当
| 6b |
| a |
| 6a |
| b |
| 6 |
| 5 |
故选A
点评：本题综合地考查了线性规划问题和由基本不等式求函数的最值问题．要求能准确地画出不等式表示的平面区域，并且能够求得目标函数的最值．
练习册系列答案
相关题目