题目内容
14.设n∈N*,圆Cn:(x-$\frac{1}{n}$)2+(y-1)2=$\frac{{4}^{n+1}-1}{{4}^{n+1}+2}$的面积为Sn,则$\underset{lim}{n→∞}$Sn=π.分析 根据圆的方程可得出圆的半径,从而可以求出圆的面积${S}_{n}=\frac{π({4}^{n+1}-1)}{{4}^{n+1}+2}$,在求极限时,分子分母同除以4n+1,然后求数列极限即可.
解答 解:根据圆的标准方程得圆的面积${S}_{n}=\frac{π({4}^{n+1}-1)}{{4}^{n+1}+2}$;
∴$\underset{lim}{n→∞}{S}_{n}=\underset{lim}{n→∞}\frac{π({4}^{n+1}-1)}{{4}^{n+1}+2}$=$\underset{lim}{n→∞}\frac{π(1-\frac{1}{{4}^{n+1}})}{1+\frac{2}{{4}^{n+1}}}$=$\frac{π(1-0)}{1+0}=π$.
故答案为:π.
点评 考查圆的标准方程,圆的面积公式,以及数列极限的概念及求法.

练习册系列答案
相关题目
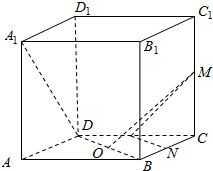 在单位正方体ABCD-A1B1C1D1中,M、N、P分别是CC1、BC,CD的中点,O为底面ABCD的中心.
在单位正方体ABCD-A1B1C1D1中,M、N、P分别是CC1、BC,CD的中点,O为底面ABCD的中心.