题目内容

(1)an = 2n-1(n∈N*)
(2)A∩B =" {" 1 }
(1)∵ 数列{ an }的前n项和为Sn = 2n+1-n-2,
∴ a1 =" S1" = 21+1-1-2 = 1. …………………… 1分
当n≥2时,有 an = Sn-Sn-1 =
(2n+1-n-2)-[ 2n-(n-1)-2 ] = 2n-1. …………………… 4分
又 ∵ n = 1时,也满足an = 2n-1,
∴ 数列{ an }的通项公式为 an = 2n-1(n∈N*). ………………… 6分
(2)∵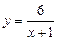 ,x、y∈N*,∴ 1 + x = 1,2,3,6,
,x、y∈N*,∴ 1 + x = 1,2,3,6,
于是 x = 0,1,2,5, 而 x∈N*,∴ B =" {" 1,2,5 }. ………………… 9分
∵ A =" {" 1,3,7,15,…,2n-1 },∴ A∩B =" {" 1 }. …………………… 12分
∴ a1 =" S1" = 21+1-1-2 = 1. …………………… 1分
当n≥2时,有 an = Sn-Sn-1 =
(2n+1-n-2)-[ 2n-(n-1)-2 ] = 2n-1. …………………… 4分
又 ∵ n = 1时,也满足an = 2n-1,
∴ 数列{ an }的通项公式为 an = 2n-1(n∈N*). ………………… 6分
(2)∵
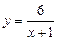 ,x、y∈N*,∴ 1 + x = 1,2,3,6,
,x、y∈N*,∴ 1 + x = 1,2,3,6,于是 x = 0,1,2,5, 而 x∈N*,∴ B =" {" 1,2,5 }. ………………… 9分
∵ A =" {" 1,3,7,15,…,2n-1 },∴ A∩B =" {" 1 }. …………………… 12分

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 的通项公式;
的通项公式;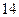 分)
分)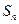 是数列
是数列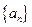 的前
的前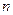 项和,点
项和,点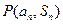
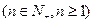 在直线
在直线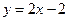 上.
上.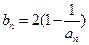 ,数列
,数列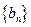 的前
的前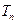 ,求使
,求使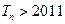 的
的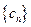 满足
满足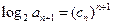 ,求数列
,求数列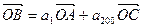 ,且A、B、C
,且A、B、C .101 C.200 D.201
.101 C.200 D.201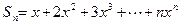 (
(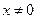 )
) 是等差数列,
是等差数列, 是各项为正
是各项为正 数的等比数列,且
数的等比数列,且 ,
, ,
, .
.  ,求数列
,求数列 的前
的前 项和
项和 .
. +
+ +
+ +……+
+……+ ,则Sn=
,则Sn= 
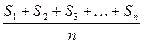 称为数列{an}的“均和”.现有一个共2010项的数列{an}:a1,a2,a3,…,a2009,a2010若其“均和”为2011,则有2011项的数列1,a1,a2,a3,…,a2009,a2010的“均和”为 .
称为数列{an}的“均和”.现有一个共2010项的数列{an}:a1,a2,a3,…,a2009,a2010若其“均和”为2011,则有2011项的数列1,a1,a2,a3,…,a2009,a2010的“均和”为 .