题目内容
已知(1-2x)n=a0+a1x+a2x2+…+anxn,且a3:a5=1:4.
(Ⅰ)求a0+a1+a2+…+an;
(Ⅱ)求(x+
)n中的常数项.
(Ⅰ)求a0+a1+a2+…+an;
(Ⅱ)求(x+
| 1 | |||
|
(Ⅰ)∵
=
,
∴
=
,
∴
=
,
解得n=8,
∴a0+a1+a2+…+an=a0+a1+a2+…+a8=(1-2×1)8=1
(Ⅱ)由(Ⅰ)知n=8,
∴Tr+1=
x8-r(
)r=
x8-
,
令8-
=0,得r=6,
∴(x+
)n中的常数项为T7=
=28.
| a3 |
| a5 |
| 1 |
| 4 |
∴
| ||
|
| 1 |
| 4 |
∴
| C | 3n |
| C | 5n |
解得n=8,
∴a0+a1+a2+…+an=a0+a1+a2+…+a8=(1-2×1)8=1
(Ⅱ)由(Ⅰ)知n=8,
∴Tr+1=
| C | r8 |
| 1 | |||
|
| C | r8 |
| 4r |
| 3 |
令8-
| 4r |
| 3 |
∴(x+
| 1 | |||
|
| C | 68 |

练习册系列答案
相关题目
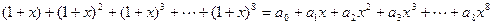 ,
,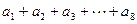 = .
= .