题目内容
【题目】下列说法正确的是( )
A.两条相交直线在同一平面内的射影必为相交直线
B.不共线三点到平面
的距离相等，则这三点确定的平面不一定与平面平行
C.对确定的两异面直线，过空间任一点有且只有一个平面与两异面直线都平行
D.两个相交平面的交线是一条线段
【答案】B
【解析】
根据空间直线与平面的关系逐一判断，选项A，若两相交直线所在平面与已知平面垂直，则两条相交直线在平面内的射影必为同一条直线；选项B若不共线的三点不在平面的同侧，这三点确定的平面与平面
相交；选项C，若点在两异面直线上，满足条件的平面不存在；选项D，根据平面的性质，即可判断真假.
选项A，若平面
平面
，平面
平面
，
则平面内任意两条相交的直线在平面内投影为直线
，
所以A错误；
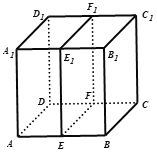
选项B，如下图在正方体
中，
分别为棱
的中点，
设平面
为平面，
三点到平面的距离相等，
三点确定的平面
与平面相交，
所以B正确；
选项C，若点
在其中的一条异面直线
上，
则过点的任一平面与直线相交，所以C错误；
选项D，因为平面是无限延伸的，所以两相交平面的交线是直线，
所以D错误.
故选：B.
练习册系列答案
相关题目
