题目内容
10.在△ABC中,角A,B,C所对的边分别为a,b,c.已知$\overrightarrow{m}$=(cos$\frac{3A}{2}$,sin$\frac{3A}{2}$),$\overrightarrow{n}$=(cos$\frac{A}{2}$,sin$\frac{A}{2}$).(1)若|$\overrightarrow{m}$+$\overrightarrow{n}$|=$\sqrt{3}$,求角A的大小;若函数f(x)=5sin(2x-$\frac{π}{6}$)的图象向右平移A个单位后对应的函数为g(x),求g(x)的图象离原点最近的对称中心;
(2)若f(x)=$\overrightarrow{m}$•$\overrightarrow{n}$-2a|$\overrightarrow{m}$+$\overrightarrow{n}$|的最小值是-$\frac{3}{2}$,试求a的值.
分析 (1)由已知向量的坐标求得斜率的模,再由|$\overrightarrow{m}$+$\overrightarrow{n}$|=$\sqrt{3}$,两边平方后可得A的值.然后利用函数的图象平移求得g(x)则g(x)的图象离原点最近的对称中心可求;
(2)求出|$\overrightarrow{m}$+$\overrightarrow{n}$|,结合(1)中求出的$\overrightarrow{m}$•$\overrightarrow{n}$可得f(x),换元后利用二次函数的最小值为-$\frac{3}{2}$求a的值.
解答 解:(1)∵$\overrightarrow{m}$=(cos$\frac{3A}{2}$,sin$\frac{3A}{2}$),$\overrightarrow{n}$=(cos$\frac{A}{2}$,sin$\frac{A}{2}$),
∴$|\overrightarrow{m}|=|\overrightarrow{n}|=1$,
由|$\overrightarrow{m}$+$\overrightarrow{n}$|=$\sqrt{3}$,得$|\overrightarrow{m}{|}^{2}+2\overrightarrow{m}•\overrightarrow{n}+|\overrightarrow{n}{|}^{2}=3$,即$\overrightarrow{m}•\overrightarrow{n}=\frac{1}{2}$,
∴$cos\frac{3A}{2}cos\frac{A}{2}+sin\frac{3A}{2}sin\frac{A}{2}=cosA=\frac{1}{2}$,
∵0<A<π,∴A=$\frac{π}{3}$.
函数f(x)=5sin(2x-$\frac{π}{6}$)的图象向右平移$\frac{π}{3}$个单位后对应的函数为g(x),
则g(x)=$5sin[2(x-\frac{π}{3})-\frac{π}{6}]=5sin(2x-\frac{5π}{6})$,
由$2x-\frac{5π}{6}=kπ$,得$x=\frac{5π}{12}+\frac{kπ}{2},k∈Z$.
取k=-1,得图象离原点最近的对称中心为(-$\frac{π}{12},0$);
(2)$\overrightarrow{m}$•$\overrightarrow{n}$=cosA,|$\overrightarrow{m}$+$\overrightarrow{n}$|=$\sqrt{2+2cosA}=2cos\frac{A}{2}$,
∴f(x)=$\overrightarrow{m}$•$\overrightarrow{n}$-2a|$\overrightarrow{m}$+$\overrightarrow{n}$|=cosA-2acos$\frac{A}{2}$=$2co{s}^{2}\frac{A}{2}-2acos\frac{A}{2}-1$.
令t=cos$\frac{A}{2}$,
∵0<A<π,∴0$<\frac{A}{2}<\frac{π}{2}$,则t∈(0,1),
∴函数f(x)化为g(t)=2t2-2at-1(0<t<1),
对称轴方程为t=$\frac{a}{2}$,
当0$<\frac{a}{2}<1$,即0<a<2时,g(t)有最小值为$2×(\frac{a}{2})^{2}-2a×\frac{a}{2}-1=-\frac{3}{2}$,
解得:a=1.
点评 本题考查平面向量的数量积运算,考查了三角函数的图象和性质,训练了学生的计算能力,是中档题.

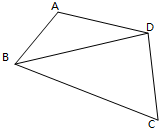 如图,在四边形ABCD中,BC=6,AD=CD=4,∠A+∠C=π,记△BCD,△ABD的面积分别为S1,S2,求S1-S2的最大值.
如图,在四边形ABCD中,BC=6,AD=CD=4,∠A+∠C=π,记△BCD,△ABD的面积分别为S1,S2,求S1-S2的最大值.