题目内容
已知:函数f(x)=a•lnx+bx2+x在点(f,f(1))处的切线方程为x-y-1=0.
(1)求f(x)的表达式;
(2)设函数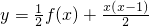 的反函数为p(x),t(x)=p(x)(1-x),求函数t(x)的最大值;
的反函数为p(x),t(x)=p(x)(1-x),求函数t(x)的最大值;
(3)在(2)中,问是否存在正整数N,使得当n∈N+且n>N时,不等式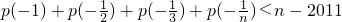 恒成立?若存在,请找出一个满足条件的N的值,并给以说明;若不存在,请说明理由.
恒成立?若存在,请找出一个满足条件的N的值,并给以说明;若不存在,请说明理由.
解:(1)当x=1时,y=0,代入f(x)=a•lnx+bx2+x得b=-1,
f′(x)= -2x+1,由切线方程知f′(1)=1,∴a=2,
-2x+1,由切线方程知f′(1)=1,∴a=2,
故f(x)=2lnx-x2+x.
(2)由(1)得函数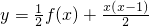 =lnx,它的反函数为p(x)=ex,
=lnx,它的反函数为p(x)=ex,
∴t(x)=ex•(1-x),
∴t′(x)=-ex•x,
当t′(x)=0时,x=0,当t′(x)>0时,x>0,当t′(x)<0时,x<0.
∴t(x)=ex•(1-x)在区间(-∞,0)上是减函数,在区间(0,+∞)上是增函数,
∴当x=0时,函数t(x)的最大值为1.
(3)由(2)得p(x)(1-x)≤1,
∴当x<1时,有p(x)≤
不等式
= +
+ +
+ +…+
+…+
=(1- )+(1-
)+(1- )+(1-
)+(1- )+…(1-
)+…(1- )
)
=n-( +
+ +
+ +…+
+…+ )≈n-ln(n+1)+C(C=0.57722…一个无理数,称作欧拉初始)
)≈n-ln(n+1)+C(C=0.57722…一个无理数,称作欧拉初始)
当n-ln(n+1)+C<n-2010时,原不等式恒成立,
故只须ln(n+1)>2010+C,即n+1>e2010+C,也即n>e2010+C-1,
故取N=[e2010+C],当n>N时,不等式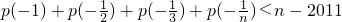 恒成立.
恒成立.
分析:(1)当x=1时,y=0,代入f(x)=a•lnx+bx2+x得b=-1,再利用切线的几何意义求得a值,最后写出函数的解析式即可;
(2)由(1)得函数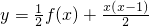 =lnx,它的反函数为p(x)=ex,求其导数,利用导数大于0原函数是增函数,导数小于0原函数是减函数,进而求出函数t(x)的最大值.
=lnx,它的反函数为p(x)=ex,求其导数,利用导数大于0原函数是增函数,导数小于0原函数是减函数,进而求出函数t(x)的最大值.
(3)由(2)得p(x)(1-x)≤1,从而有当x<1时,有p(x)≤ ,将原不等式转化成不等式n-(
,将原不等式转化成不等式n-( +
+ +
+ +…+
+…+ )<n-2010,利用调和级数的和,从而得到取N=[e2010+C],当n>N时,不等式
)<n-2010,利用调和级数的和,从而得到取N=[e2010+C],当n>N时,不等式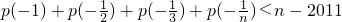 恒成立.
恒成立.
点评:本小题主要考查函数单调性的应用、利用导数研究曲线上某点切线方程、反函数、不等式的证明等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.
f′(x)=
 -2x+1,由切线方程知f′(1)=1,∴a=2,
-2x+1,由切线方程知f′(1)=1,∴a=2,故f(x)=2lnx-x2+x.
(2)由(1)得函数
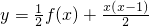 =lnx,它的反函数为p(x)=ex,
=lnx,它的反函数为p(x)=ex,∴t(x)=ex•(1-x),
∴t′(x)=-ex•x,
当t′(x)=0时,x=0,当t′(x)>0时,x>0,当t′(x)<0时,x<0.
∴t(x)=ex•(1-x)在区间(-∞,0)上是减函数,在区间(0,+∞)上是增函数,
∴当x=0时,函数t(x)的最大值为1.
(3)由(2)得p(x)(1-x)≤1,
∴当x<1时,有p(x)≤

不等式

=
 +
+ +
+ +…+
+…+
=(1-
 )+(1-
)+(1- )+(1-
)+(1- )+…(1-
)+…(1- )
)=n-(
 +
+ +
+ +…+
+…+ )≈n-ln(n+1)+C(C=0.57722…一个无理数,称作欧拉初始)
)≈n-ln(n+1)+C(C=0.57722…一个无理数,称作欧拉初始)当n-ln(n+1)+C<n-2010时,原不等式恒成立,
故只须ln(n+1)>2010+C,即n+1>e2010+C,也即n>e2010+C-1,
故取N=[e2010+C],当n>N时,不等式
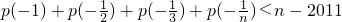 恒成立.
恒成立.分析:(1)当x=1时,y=0,代入f(x)=a•lnx+bx2+x得b=-1,再利用切线的几何意义求得a值,最后写出函数的解析式即可;
(2)由(1)得函数
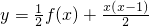 =lnx,它的反函数为p(x)=ex,求其导数,利用导数大于0原函数是增函数,导数小于0原函数是减函数,进而求出函数t(x)的最大值.
=lnx,它的反函数为p(x)=ex,求其导数,利用导数大于0原函数是增函数,导数小于0原函数是减函数,进而求出函数t(x)的最大值.(3)由(2)得p(x)(1-x)≤1,从而有当x<1时,有p(x)≤
 ,将原不等式转化成不等式n-(
,将原不等式转化成不等式n-( +
+ +
+ +…+
+…+ )<n-2010,利用调和级数的和,从而得到取N=[e2010+C],当n>N时,不等式
)<n-2010,利用调和级数的和,从而得到取N=[e2010+C],当n>N时,不等式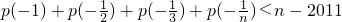 恒成立.
恒成立.点评:本小题主要考查函数单调性的应用、利用导数研究曲线上某点切线方程、反函数、不等式的证明等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.

练习册系列答案
相关题目