题目内容
[x]表示不超过x的最大整数,定义函数f(x)=x-[x].则下列结论中正确的有
①函数f(x)的值域为[0,1]
②方程f(x)=
有无数个解
③函数f(x)的图象是一条直线
④函数f(x)在区间[k,k+1)(k∈Z)上是增函数.
②④
②④
①函数f(x)的值域为[0,1]
②方程f(x)=
| 1 | 2 |
③函数f(x)的图象是一条直线
④函数f(x)在区间[k,k+1)(k∈Z)上是增函数.
分析:因为[x]表示不超过x的最大整数,研究函数的周期性和值域,据此画出函数的图象,从而使问题得到解决.
解答:解:∵{x+1}=(x+1)-[x+1]=x-[x]={x},
∴函数{x}=x-[x]是周期为1的函数,
当0≤x<1时,{x}=x-[x]=x-0=x,
∴函数{x}的值域为[0,1),故①错误;
当x=
时,{x}=
,又∵函数{x}=x-[x]是周期为1的函数,
∴x=
+k时(k∈Z),{x}=
,∴②是正确的,
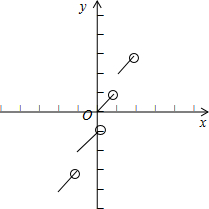
由上图可知③错误;④正确.
故答案为:②④
∴函数{x}=x-[x]是周期为1的函数,
当0≤x<1时,{x}=x-[x]=x-0=x,
∴函数{x}的值域为[0,1),故①错误;
当x=
| 1 |
| 2 |
| 1 |
| 2 |
∴x=
| 1 |
| 2 |
| 1 |
| 2 |
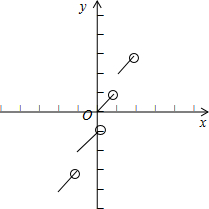
由上图可知③错误;④正确.
故答案为:②④
点评:本题考查新定义的情况下,对函数的性质的应用,数形结合是就问题的关键,属基础题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目