题目内容
直线y=kx+1与椭圆 的位置关系是
的位置关系是
- A.相交
- B.相切
- C.相离
- D.不确定
A
分析:直线y=kx+1过定点(0,1),而(0,1)恰在椭圆 内,从而答案选A.
内,从而答案选A.
解答:∵直线y=kx+1过定点(0,1),把(0,1)代入椭圆方程的左端有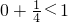 ,即(0,1)在椭圆内部,
,即(0,1)在椭圆内部,
∴直线y=kx+1与椭圆 必相交,
必相交,
因此可排除B、C、D;
故选A.
点评:本题考查直线与椭圆的位置关系,解决的捷径在于观察到直线y=kx+1过定点(0,1),而该点恰在已知的椭圆的内部,从而使问题得以解决,属于容易题.若联立两个方程,用判别式解决,行但麻烦,则是小题大作.
分析:直线y=kx+1过定点(0,1),而(0,1)恰在椭圆
 内,从而答案选A.
内,从而答案选A.解答:∵直线y=kx+1过定点(0,1),把(0,1)代入椭圆方程的左端有
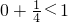 ,即(0,1)在椭圆内部,
,即(0,1)在椭圆内部,∴直线y=kx+1与椭圆
 必相交,
必相交,因此可排除B、C、D;
故选A.
点评:本题考查直线与椭圆的位置关系,解决的捷径在于观察到直线y=kx+1过定点(0,1),而该点恰在已知的椭圆的内部,从而使问题得以解决,属于容易题.若联立两个方程,用判别式解决,行但麻烦,则是小题大作.

练习册系列答案
相关题目