题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() ,求曲线
,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)若对任意的![]() ,
,![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)对![]() 求导得到
求导得到![]() ,代入
,代入![]() ,得到切线的斜率,结合切点,得到切线方程;(2)根据题意,得到
,得到切线的斜率,结合切点,得到切线方程;(2)根据题意,得到![]() ,然后利用参变分离,得到
,然后利用参变分离,得到![]() ,设
,设![]() ,利用导数得到
,利用导数得到![]() 的最小值,从而得到
的最小值,从而得到![]() 的范围.
的范围.
(1)因为![]() ,所以函数
,所以函数![]() ,
,
所以![]() ,即切点为
,即切点为![]()
所以![]() ,
,
代入![]() ,得到
,得到![]() ,
,
故所求的切线方程为![]() ,
,
即![]() .
.
(2)对任意的![]() ,
,![]() ,
,![]() 恒成立,
恒成立,
可得![]() ,对任意的
,对任意的![]() ,
,![]() 恒成立,
恒成立,
![]() ,令
,令![]() 得
得![]() 或
或![]() ,
,
所以![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
而![]() ,
,![]() ,所以
,所以![]() ,
,
所以![]() ,对任意的
,对任意的![]() 恒成立,
恒成立,
即![]() 对任意的
对任意的![]() 恒成立,
恒成立,
所以![]() ,对任意的
,对任意的![]() 恒成立,
恒成立,
设![]() ,
,![]() ,则
,则![]()
![]() ,
,
设![]() ,
,![]()
因为![]() ,所以
,所以![]() ,所以
,所以![]() 单调递增,
单调递增,
即![]() 单调递增,而
单调递增,而![]() ,
,
所以当![]() ,
,![]() ,
,![]() 单调递减,
单调递减,
当![]() ,
,![]() ,
,![]() 单调递增,
单调递增,
所以![]() 时,
时,![]() 取得最小值,为
取得最小值,为![]() ,
,
所以![]() .
.

练习册系列答案
相关题目
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式,为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人.第一组工人用第一种生产方式,第二组工人用第二种生产方式,根据工人完成生产任务的工作时间(单位:min)绘制了如图所示的茎叶图:
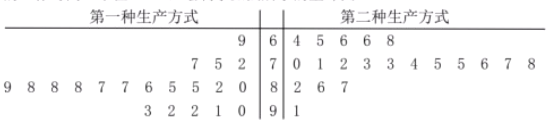
(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求40名工人完成生产任务所需时间的中位数,并将完成生产任务所需时间超过和不超过的工人数填入下面的列联表,再根据列联表,能否有99.9%的把握认为两种生产方式的效率有差异?
超过 | 不超过 | |
第一种生产方式 | ||
第二种生产方式 |
附: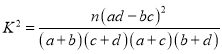 ,
,
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |