题目内容
已知函数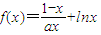 .
.(1)当a=1时,求f(x)的最小值;
(2)若函数
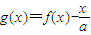 在区间(1,2)上不单调,求a的取值范围.
在区间(1,2)上不单调,求a的取值范围.
【答案】分析:(1)当a=1时,准确求出函数的导数是解决本题的关键,求函数的最值要研究函数在定义区间的单调性,通过函数的单调性解决本题;
(2)将函数在给定区间上不单调问题进行等价转化是解决本题的关键,即将原函数不单调问题转化为导函数在给定区间上有根问题,利用分离常数法解决本题.
解答:解:(1)当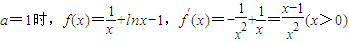 ,
,
令f′(x)=0得x=1.f′(x)<0得0<x<1,f′(x)>0得1<x,
∴f(x)在(0,1)上单调递减,在(1,+∞)上单调递增.
故fmin(x)=f(1)=0.
(2)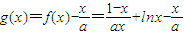 .
.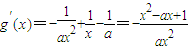 .
.
∵g(x)在(1,2)上不单调,
∴x2-ax+1=0在(1,2)上有根且无重根.
即方程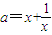 在(1,2)有根,且无重根.
在(1,2)有根,且无重根.
∴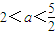 .
.
点评:本题考查导数研究函数的最值、单调性等问题,考查学生的转化与化归思想,求最值时候要注意研究函数的单调性,将函数的单调性问题转化为导函数的正负问题,本题又一个考点是利用分离常数法求字母的取值范围,将字母的取值范围转化为相应函数的值域问题,通过求函数的值域达到解决本题的目的.
(2)将函数在给定区间上不单调问题进行等价转化是解决本题的关键,即将原函数不单调问题转化为导函数在给定区间上有根问题,利用分离常数法解决本题.
解答:解:(1)当
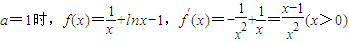 ,
,令f′(x)=0得x=1.f′(x)<0得0<x<1,f′(x)>0得1<x,
∴f(x)在(0,1)上单调递减,在(1,+∞)上单调递增.
故fmin(x)=f(1)=0.
(2)
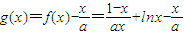 .
.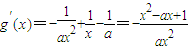 .
.∵g(x)在(1,2)上不单调,
∴x2-ax+1=0在(1,2)上有根且无重根.
即方程
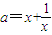 在(1,2)有根,且无重根.
在(1,2)有根,且无重根.∴
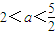 .
.点评:本题考查导数研究函数的最值、单调性等问题,考查学生的转化与化归思想,求最值时候要注意研究函数的单调性,将函数的单调性问题转化为导函数的正负问题,本题又一个考点是利用分离常数法求字母的取值范围,将字母的取值范围转化为相应函数的值域问题,通过求函数的值域达到解决本题的目的.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 .
. 的极小值;
的极小值; ,x∈[-1,1],求
,x∈[-1,1],求 的最大值F(a).
的最大值F(a). .
. 时,f(x)的值域为[4,6],求a,b的值.
时,f(x)的值域为[4,6],求a,b的值. 函数
函数 .
.