Question

【题目】已知椭圆的离心率为,抛物线的焦点是,是抛物线上的点,H为直线上任一点,A,B分别为椭圆C的上下顶点,且A,B,H三点的连线可以构成三角形.

(Ⅰ)求椭圆C的方程;

(Ⅱ)直线HA,HB与椭圆C的另一交点分别为点D,E,求证:直线DE过定点.

Answer 1

【答案】(Ⅰ) . (Ⅱ)见解析

【解析】

(Ⅰ)先求出抛物线方程，然后列出的方程组，解之得椭圆标准方程．

(Ⅱ) 设点，求得方程，与椭圆联立求得坐标，写出直线方程，由方程观察得定点．

解(Ⅰ)由抛物线焦点为,得抛物线方程为

由题意知,,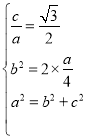

解得,

∴椭圆C的方程为.

(Ⅱ)设点,易知,,

∴直线HA的方程为,直线HB的方程为.

联立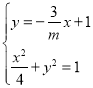,得,

∴,,同理可得,,

∴直线DE的斜率为,∴直线DE的方程为

,

即,

∴直线过定点.

即直线DE过定点.