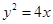题目内容
(本小题满分12分)
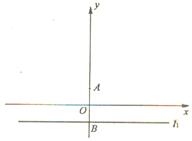
已知定点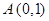 ,直线
,直线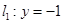 交
交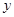 轴于点
轴于点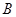 ,记过点
,记过点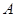 且与直线
且与直线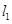 相切的圆的圆心为点
相切的圆的圆心为点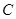 .
.
(I)求动点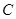 的轨迹
的轨迹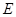 的方程;
的方程;
(Ⅱ)设倾斜角为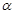 的直线
的直线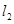 过点
过点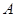 ,交轨迹
,交轨迹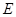 于两点
于两点 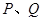 ,交直线
,交直线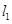 于点
于点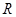 .若
.若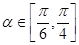 ,求
,求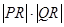 的最小值.
的最小值.
已知定点
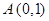 ,直线
,直线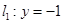 交
交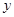 轴于点
轴于点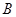 ,记过点
,记过点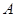 且与直线
且与直线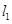 相切的圆的圆心为点
相切的圆的圆心为点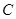 .
.
(I)求动点
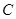 的轨迹
的轨迹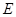 的方程;
的方程;(Ⅱ)设倾斜角为
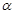 的直线
的直线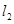 过点
过点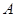 ,交轨迹
,交轨迹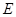 于两点
于两点 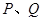 ,交直线
,交直线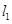 于点
于点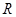 .若
.若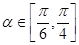 ,求
,求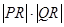 的最小值.
的最小值.(I) 
(Ⅱ) |PR|·|QR|的最小值为16

(Ⅱ) |PR|·|QR|的最小值为16
本试题主要是考查了抛物线的方程的求解,以及直线与抛物线的位置关系的综合运用。
(1)连CA,过C作CD⊥l1,垂足为D,由已知可得|CA|=|CD|,
∴点C的轨迹是以A为焦点,l1为准线的抛物线,
(2)设直线l2的方程为y=kx+1,
把直线方程与抛物线方程联立消去y得 x2-4kx-4=0.
结合韦达定理来表示关系式,以向量的数量积来表示模长的积,得到结论。
解法一:(Ⅰ)连CA,过C作CD⊥l1,垂足为D,由已知可得|CA|=|CD|,
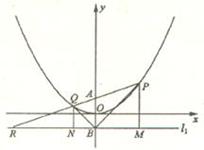
∴点C的轨迹是以A为焦点,l1为准线的抛物线,
∴轨迹E的方程为 ………6分
………6分
(Ⅱ)设直线l2的方程为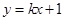 ,与抛物线方程联立消去y得x2-4kx-4=0.
,与抛物线方程联立消去y得x2-4kx-4=0.
记P(x1,y1),Q(x2,y2),则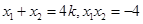 .
.
因为直线PA的斜率k≠O,易得点R的坐标为 .
.
|PR|·|QR|=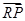 ·
·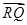 =(x1+
=(x1+ ,y1+1)·(x2+
,y1+1)·(x2+ ,y2+1)
,y2+1)
=(x1+ )(x2+
)(x2+ )+(kx1+2 )(kx2+ 2)
)+(kx1+2 )(kx2+ 2)
=(1+k2) x1 x2+( +2 k)( x1+x2)+
+2 k)( x1+x2)+ 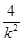 +4
+4
= -4(1+k2)+4k( +2k)+
+2k)+ 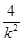 +4
+4
=4(k2+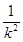 )+8,
)+8,
∵k2+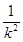 ≥2,当且仅当k2=1时取到等号.
≥2,当且仅当k2=1时取到等号.
又α∈[ ,
,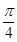 ],k∈[
],k∈[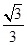 ,1],∴上述不等式中等号能取到.
,1],∴上述不等式中等号能取到.
从而|PR|·|QR|的最小值为16. ………12分
解法二:(I)同解法一.
(Ⅱ)设直线l2的方程为y=kx+1,
把直线方程与抛物线方程联立消去y得 x2-4kx-4=0.
记P(x1,y1),Q(x2,y2),则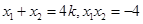 .
.
PR|·|QR|=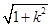 |x1-xR|·
|x1-xR|·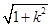 |x2-xR|
|x2-xR|
=(1+k2)·(x1+ )(x2+
)(x2+ ),
),
下同解法一.
(1)连CA,过C作CD⊥l1,垂足为D,由已知可得|CA|=|CD|,
∴点C的轨迹是以A为焦点,l1为准线的抛物线,
(2)设直线l2的方程为y=kx+1,
把直线方程与抛物线方程联立消去y得 x2-4kx-4=0.
结合韦达定理来表示关系式,以向量的数量积来表示模长的积,得到结论。
解法一:(Ⅰ)连CA,过C作CD⊥l1,垂足为D,由已知可得|CA|=|CD|,

∴点C的轨迹是以A为焦点,l1为准线的抛物线,
∴轨迹E的方程为
 ………6分
………6分(Ⅱ)设直线l2的方程为
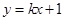 ,与抛物线方程联立消去y得x2-4kx-4=0.
,与抛物线方程联立消去y得x2-4kx-4=0.记P(x1,y1),Q(x2,y2),则
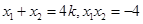 .
.因为直线PA的斜率k≠O,易得点R的坐标为
 .
.|PR|·|QR|=
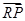 ·
·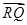 =(x1+
=(x1+ ,y1+1)·(x2+
,y1+1)·(x2+ ,y2+1)
,y2+1)=(x1+
 )(x2+
)(x2+ )+(kx1+2 )(kx2+ 2)
)+(kx1+2 )(kx2+ 2)=(1+k2) x1 x2+(
 +2 k)( x1+x2)+
+2 k)( x1+x2)+ 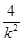 +4
+4= -4(1+k2)+4k(
 +2k)+
+2k)+ 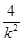 +4
+4=4(k2+
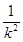 )+8,
)+8,∵k2+
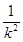 ≥2,当且仅当k2=1时取到等号.
≥2,当且仅当k2=1时取到等号.又α∈[
 ,
,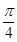 ],k∈[
],k∈[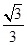 ,1],∴上述不等式中等号能取到.
,1],∴上述不等式中等号能取到.从而|PR|·|QR|的最小值为16. ………12分
解法二:(I)同解法一.
(Ⅱ)设直线l2的方程为y=kx+1,
把直线方程与抛物线方程联立消去y得 x2-4kx-4=0.
记P(x1,y1),Q(x2,y2),则
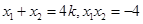 .
.PR|·|QR|=
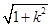 |x1-xR|·
|x1-xR|·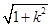 |x2-xR|
|x2-xR|=(1+k2)·(x1+
 )(x2+
)(x2+ ),
),下同解法一.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
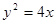 上一点
上一点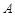 的横坐标为4,则点
的横坐标为4,则点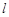 :
: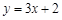 交抛物线
交抛物线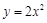 于
于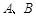 两点,
两点,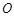 为坐标原点.
为坐标原点.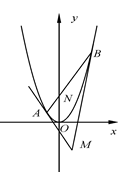
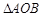 的面积;
的面积;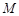 ,求点
,求点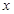 轴为对称轴,以坐标原点为顶点,准线
轴为对称轴,以坐标原点为顶点,准线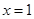 的抛物线的方程是
的抛物线的方程是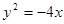
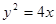
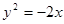
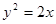
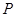 在抛物线
在抛物线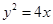 上,则点
上,则点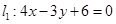 的距离和到直线
的距离和到直线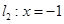 的距离之和的最小值为
的距离之和的最小值为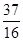
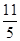
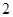
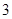
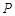 为抛物线C:
为抛物线C: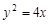 上的一点,
上的一点,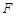 为抛物线C的焦点,其准线与
为抛物线C的焦点,其准线与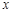 轴交于点
轴交于点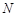 ,直线
,直线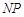 与抛物线交于另一点
与抛物线交于另一点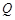 ,且
,且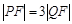 ,则点
,则点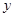 轴的右侧运动,它到
轴的右侧运动,它到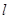 过抛物线
过抛物线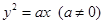 的焦点
的焦点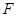 ,且和
,且和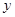 轴交于点
轴交于点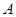 ,若
,若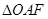 (
(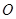 为坐标原点)的面积为4,则抛物线方程为( )
为坐标原点)的面积为4,则抛物线方程为( )