题目内容
设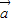 ,
,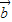 是两个不共线的向量,若
是两个不共线的向量,若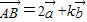 ,
,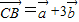 ,
,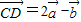 ,且A、B、D三点共线,则k= .
,且A、B、D三点共线,则k= .
【答案】分析:利用两个向量的加减法的法则,以及其几何意义求出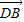 的坐标,把A、B、D三点共线转化为
的坐标,把A、B、D三点共线转化为 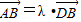 ,即
,即 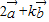 =λ(-
=λ(- )=-λ
)=-λ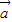 +4λ
+4λ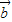 ,故有-λ=2,4λ=k,
,故有-λ=2,4λ=k,
解方程求得k的值.
解答:解:由题意可得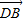 =
=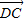 +
+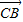 =-(
=-(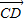 )+
)+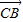 =(-2
=(-2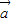 +
+ )+
)+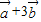 =-
=-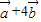 .
.
∵A、B、D三点共线,
∴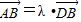 ,
,
∴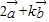 =λ(-
=λ(-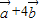 )=-λ
)=-λ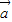 +4λ
+4λ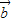 .
.
故有-λ=2,4λ=k,解得 λ=-2,k=-8.
故答案为:-8.
点评:本题主要考查证明三点共线的方法,两个向量的加减法的法则,以及其几何意义,两个向量共线的性质,体现了转化的数学思想,把A、B、D三点共线转化为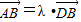 .
.
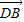 的坐标,把A、B、D三点共线转化为
的坐标,把A、B、D三点共线转化为 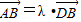 ,即
,即 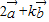 =λ(-
=λ(- )=-λ
)=-λ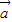 +4λ
+4λ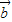 ,故有-λ=2,4λ=k,
,故有-λ=2,4λ=k,解方程求得k的值.
解答:解:由题意可得
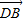 =
=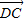 +
+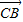 =-(
=-(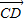 )+
)+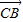 =(-2
=(-2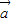 +
+ )+
)+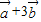 =-
=-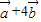 .
.∵A、B、D三点共线,
∴
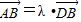 ,
,∴
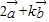 =λ(-
=λ(-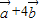 )=-λ
)=-λ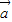 +4λ
+4λ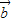 .
.故有-λ=2,4λ=k,解得 λ=-2,k=-8.
故答案为:-8.
点评:本题主要考查证明三点共线的方法,两个向量的加减法的法则,以及其几何意义,两个向量共线的性质,体现了转化的数学思想,把A、B、D三点共线转化为
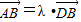 .
. 
练习册系列答案
相关题目
 为两个不共线的向量,
为两个不共线的向量,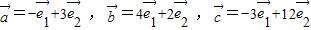 ,试用
,试用 为基底表示向量
为基底表示向量 ;
; ,当k为何值时,
,当k为何值时, ∥
∥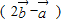 ?平行时它们是同向还是反向?
?平行时它们是同向还是反向?